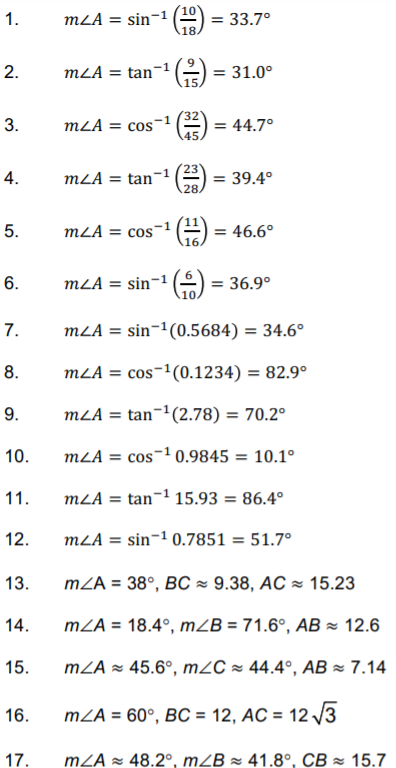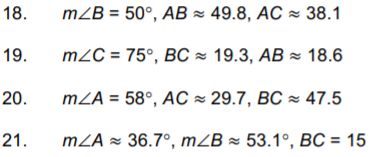10 Trigonometry
Michael Hrycay
Section Information
Outcome/Competency: You will be able to model scenarios and solve problems using trigonometry.
Timing: 26h
Rationale:
Why is it important for you to learn this skill?
Trigonometry is all about triangles. Understanding trigonometry will help calculate values in any scenario involving a triangle, and you would be surprised at how many situations can be broken down into a series of triangles. Additionally, in science, we will see quantities involving direction (like motion and force) can be broken down into components, or units of direction. Once direction is broken down into components, it is easy to do calculations and Trigonometry makes it possible.
Objectives
To be competent in this area, the individual must be able to:
- Identify the characteristics of a right-angle triangle
- Calculate the unknown side or angles of a right-angle triangle
- Calculate guying and rigging lengths and angles using trigonometry
Learning Goals
- Identify the characteristics of a right-angle triangle and calculate sides and angles
- Understand and utilize the Pythagorean Theorem to solve for the unknown side
- Model and solve problems using the appropriate trigonometric ratios and trigonometry
Introduction:
In this section you will learn about right-angle triangle properties, similar triangles, proportionality, the Pythagorean Theorem, and Trigonometric Ratios. You will learn how to use a trigonometric ratio to find unknown sides or angles. Throughout the section you will presented with concepts and examples, as well as opportunities to practice.
Topic 1: Right Angle Triangle Properties (4h)
Instructions
- Go through the content and examples in each subtopic with the group, leaving opportunities for questions.
- Have students complete the practice exercises independently, then take up the answers.
Angles
An angle is formed when two straight paths cross. Consider this story: you walk along a straight path, and so does your friend. At first you both are so far apart that you can’t see each other. But as you walk along you get closer and closer until you meet together. Your meeting place is called the vertex.
The interesting part about angles is at the beginning of the journey, you are far from your friend. Halfway through your journey, your friend is closer, and at the end of the journey there is no distance between you and your friend. Throughout the journey you were a changing distance from each other, but the angle of your paths did not change.

Notice the paths on the left form a smaller angle than the paths on the right. The size of an angle is measured in degrees.
Types of Angles
Angles can be grouped according to how large they are. Special angles are:
- The right angle: One half of a square is a right angle. Notice the right angle symbol (a small box.) The symbol for degrees is the small circle to the upper right of the number, and a right angle is 90˚ (degrees.)
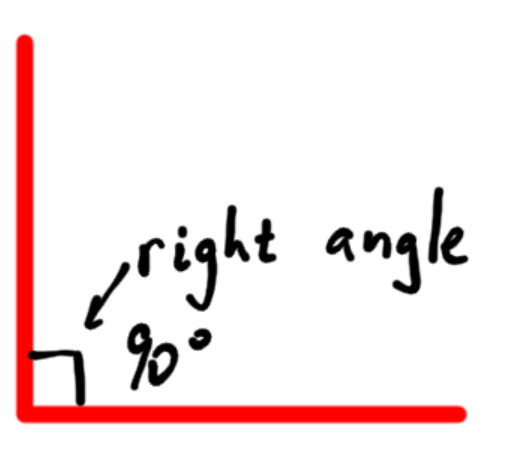
- The Straight Angle: The straight angle is essentially a line. In the story above, it would be if you and your friend were headed straight on toward each other.
- Acute Angle: An acute angle is less than 90 degrees.
- Obtuse Angle: An obtuse angle is greater than 90 degrees, but less than 180 degrees (a straight line.)
Examples:
Label the following angles:
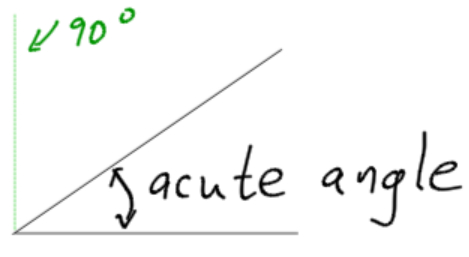
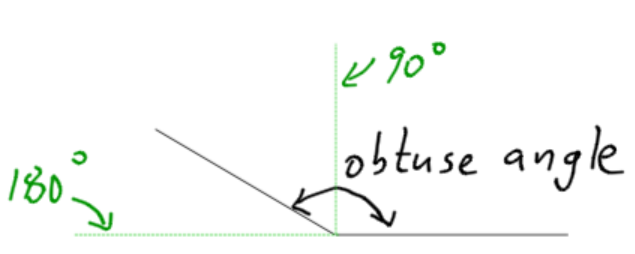
Related Angles
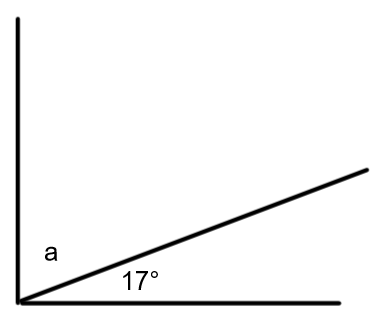
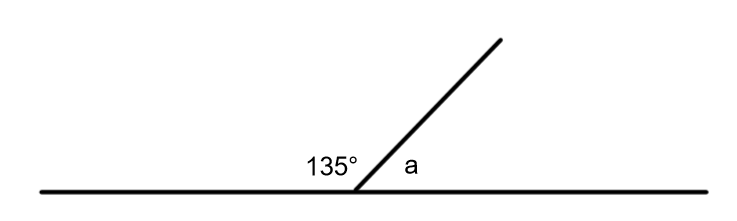
Two angles are related when they add up to either 90 or 180 degrees. Two angles that add to 90 degrees are complimentary. Two angles that add to 180 degrees are supplementary.
Examples:
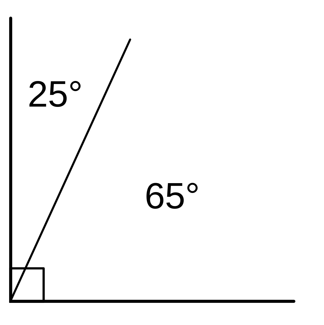
1. Angles 25˚ and 65˚ are complimentary because 25 + 65 = 90
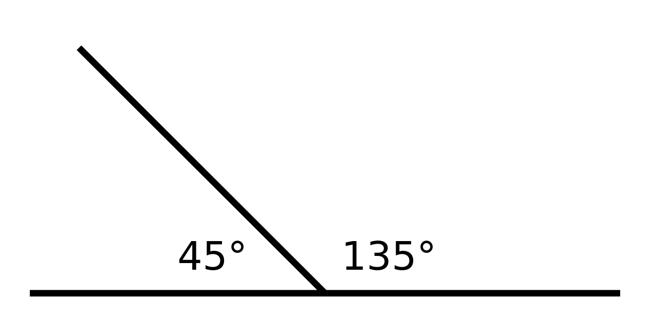
2. Angles 45˚ and 135˚ are supplementary because 45 + 135 = 180
Types of Triangles
Triangles are classified into three types: the same as angles.
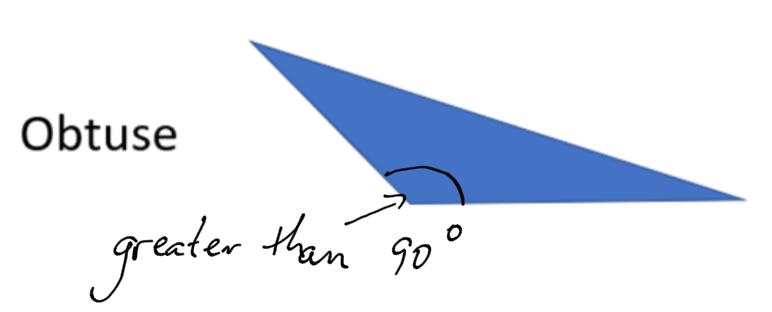
An obtuse triangle has one angle that is greater than 90 degrees (one obtuse angle.)
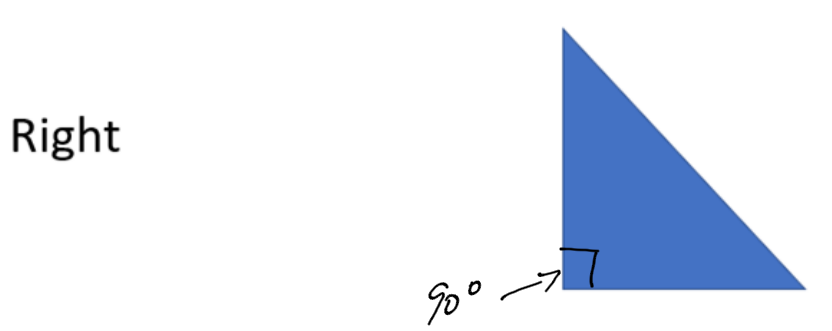
A right triangle has one angle that is exactly 90 degrees (one right angle.)
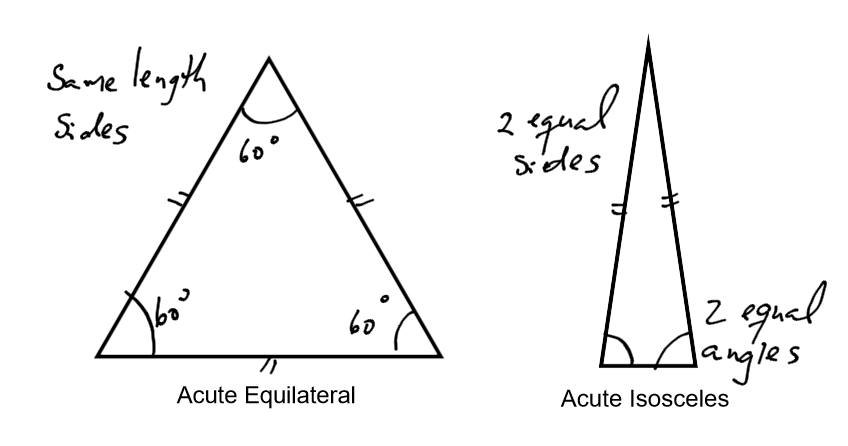
An acute triangle has all three angles less than 90 degrees (three acute angles). Above, the triangle on the left is called equilateral because all the sides are the same length. The triangle on the right is called isosceles because two of the sides are the same length.
Examples:
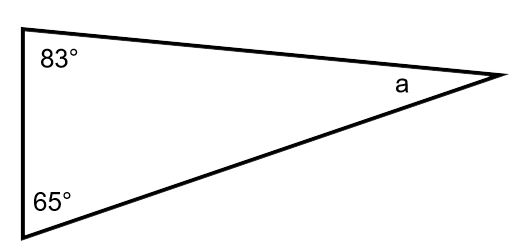
1. How large, in degrees, is the unknown angle?
a)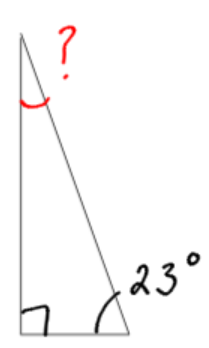
Although it isn’t written, one of the angles is 90 degrees, because it is marked with the box. The other angle is 23 degrees.
180 total degrees – 90 degrees – 23 degrees = 67 degrees. There are 67 degrees left for the unknown angle.
b)
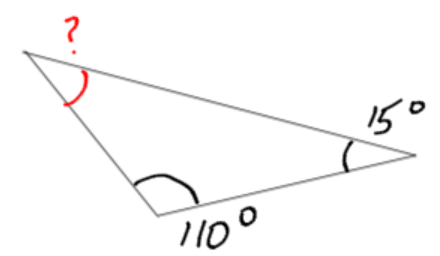
180 total degrees – 110 degrees – 15 degrees = 55 degrees. There are 55 degrees left for the unknown angle.
Practice Exercises: Right Angle Triangle Properties
1. Label the following triangles acute, isosceles, equilateral, obtuse, right.
|
a)
|
b)
|
|
c)
|
d)
|
2. Find the unknown angles:
|
a)
|
b)
|
|
c)
|
d)
|
Answer Key:
1a) right, b) obtuse, c) equilateral acute, d) isosceles acute
2a) 73, b) 45, c) 32, d) 63
Topic 2: Similar Triangles and Proportionality (4h)
Instructions
- Go through the content and examples with the group, leaving opportunities for questions.
- Have students complete the practice exercises independently, then take up the answers.
A pair of Similar Triangles is like the path mentioned in the story above. They meet at the same angle but may be larger or smaller. Specifically: Similar Triangles have the same angles, and the sides are in proportional.
Example:
The following two triangles are similar because their angles are the same:
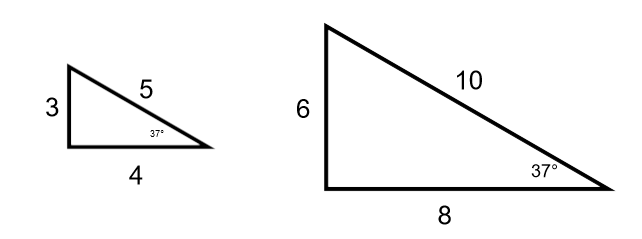
The sides are also proportional. Each side is multiplied by the same number (2) to get the larger side.
Example:
Use the proportion equation to find the unknown side of these similar triangles:
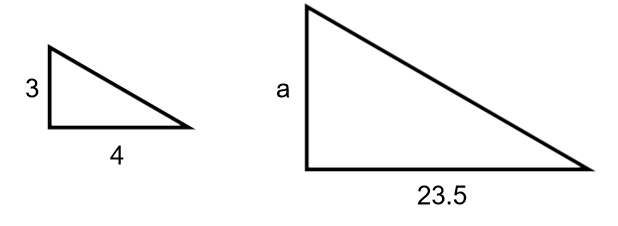
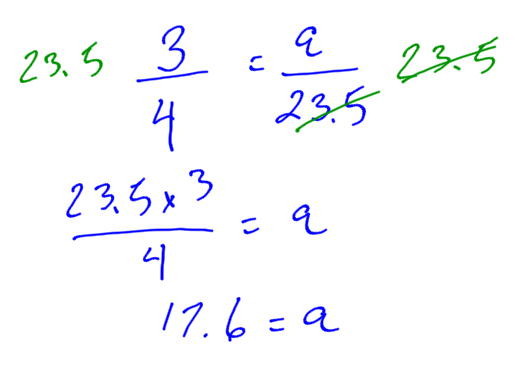
The unknown side, a, is 17.6.
Practice Exercises
1. Solve each proportion. Show your work and check your solution
a.
b.
c.
d.
2. Create a proportion for each set of similar triangles. Then solve the proportion.
 Answer Key
Answer Key
1. a. 15, b. 6, c. 3, d. 15
5.
6.
Topic 3: Pythagorean Theorem (4h)
Instructions
- Go through the content and examples with the group, leaving opportunities for questions.
- Have students complete the practice exercises independently, then take up the answers.
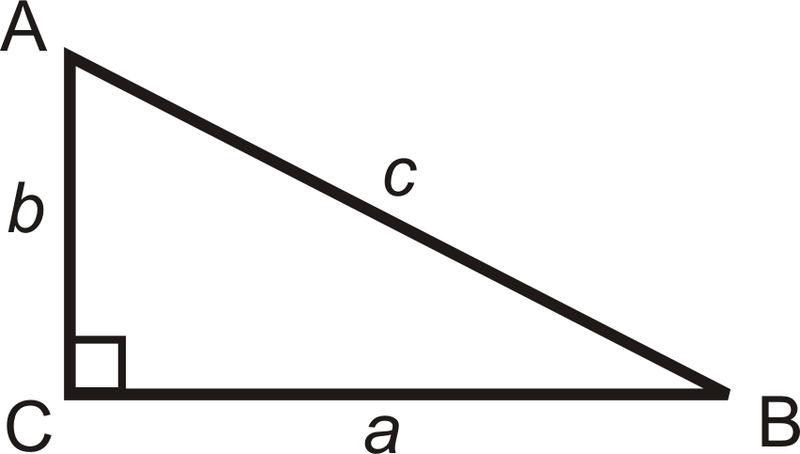
The two shorter sides of a right triangle (the sides that form the right angle) are the legs and the longer side (the side opposite the right angle) is the hypotenuse. For the Pythagorean Theorem, the legs are “a” and “b” and the hypotenuse is “c”.
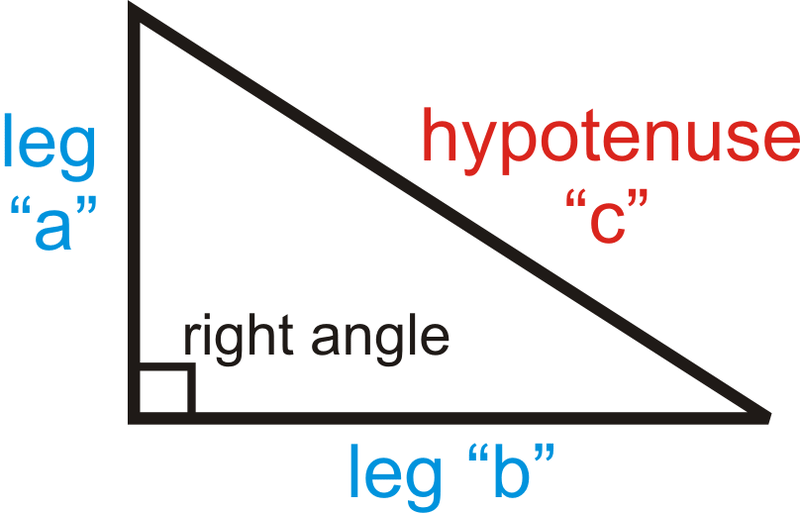
Pythagorean Theorem:
Given a right triangle with legs of lengths a and b and a hypotenuse of length c,
The converse of the Pythagorean Theorem is also true. It allows you to prove that a triangle is a right triangle even if you do not know its angle measures.
If the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
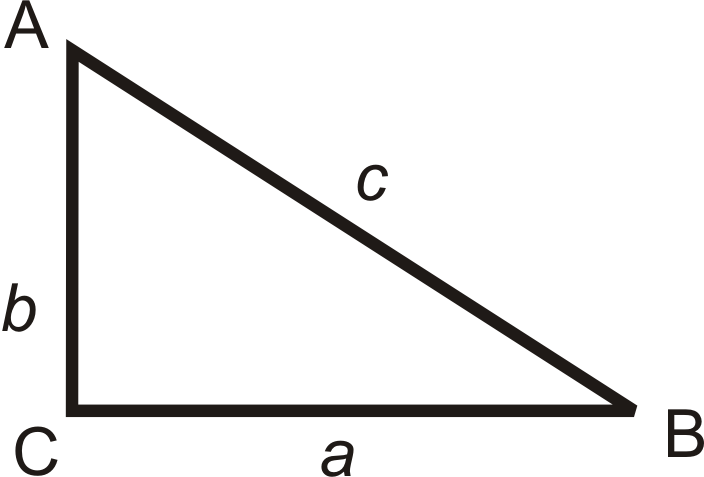
Notice in the above diagram, Labeling the triangle is as follows:
- Angles are labeled with capital letters
- Sides are labeled with small letters
- The side and the opposite angle have the same letter.
Example:
Is the following triangle a right angle triangle?
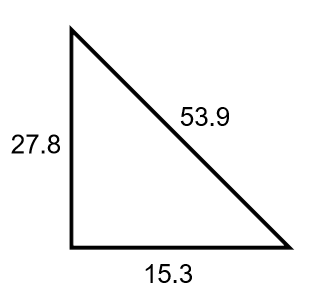
Label the sides of the triangle. The Hypotenuse must be labeled c:
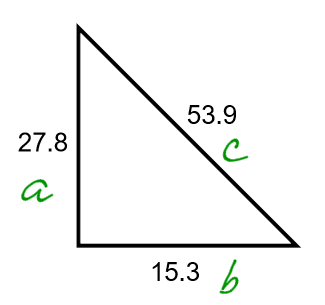
Test the Pythagorean theorem to see if both sides of the equation are equal. If both sides are equal, the triangle is a right angle triangle.
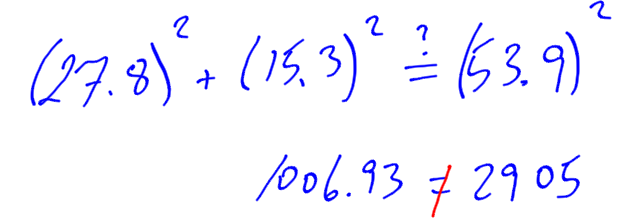
Since 1006 does not equal 2905, the triangle is not a right angle triangle.
Pythagorean Triples
A combination of three numbers that makes the Pythagorean Theorem true is called a Pythagorean triple. Each set of numbers below is a Pythagorean triple.
3,4,5
5,12,13
7,24,25
8,15,17
9,12,15
10,24,26
Any multiple of a Pythagorean triple is also considered a Pythagorean triple. Multiplying 3, 4, 5 by 2 gives 6, 8, 10, which is another triple. To see if a set of numbers makes a Pythagorean triple, plug them into the Pythagorean Theorem.
Example 1
What is the diagonal of a rectangle with sides 10 and 16?
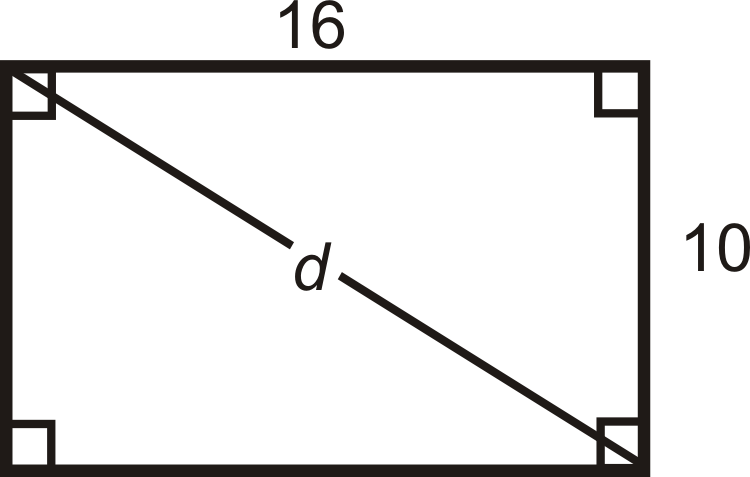
For any square and rectangle, you can use the Pythagorean Theorem to find the length of a diagonal. Plug in the sides to find d.
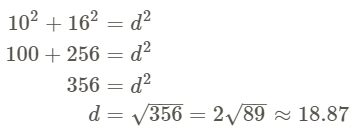
Example 2
Find the length of the hypotenuse.
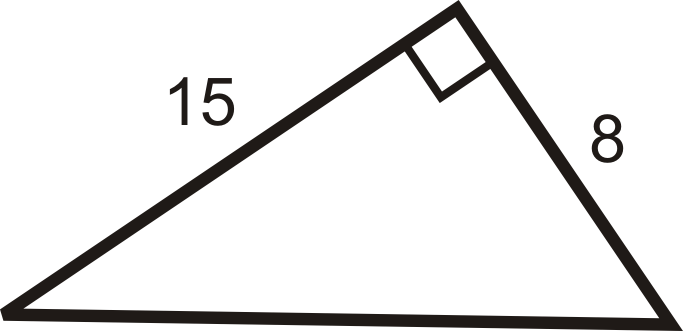
Use the Pythagorean Theorem. Set a=8 and b=15. Solve for c.
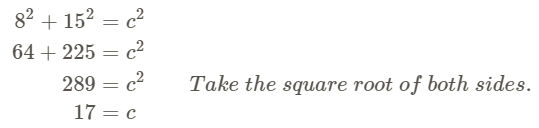
Example 3
Is 20, 21, 29 a Pythagorean triple?
If , then the set is a Pythagorean triple.
Therefore, 20, 21, and 29 is a Pythagorean triple.
Example 4
Determine if the triangles below are right triangles.
Check to see if the three lengths satisfy the Pythagorean Theorem. Let the longest side represent c.
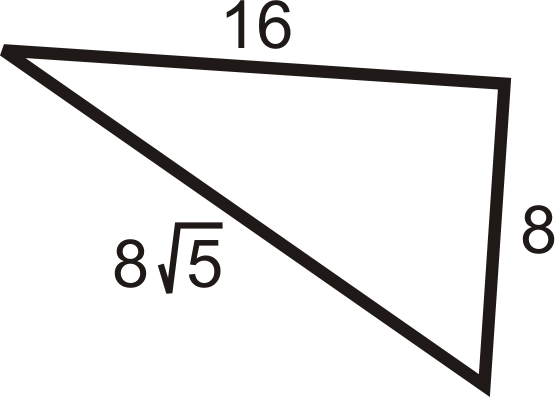
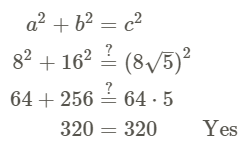
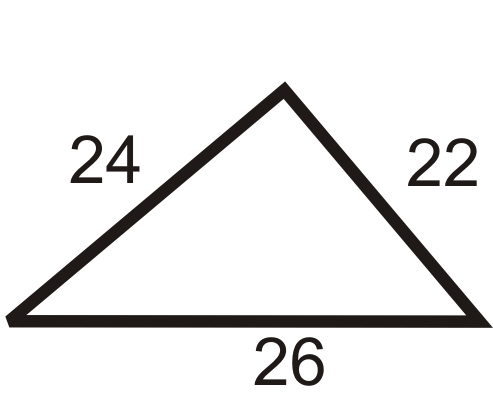
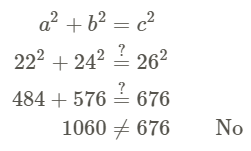
Practice Exercises
1. Determine if the following sets of numbers are Pythagorean Triples.
a) 12, 35, 37
b) 9, 17, 18
2. Determine if the following lengths make a right triangle.
a) 7, 24, 25
b) 15, 20, 25
3. Determine all the unknown sides. Which triangles are mathematically similar?
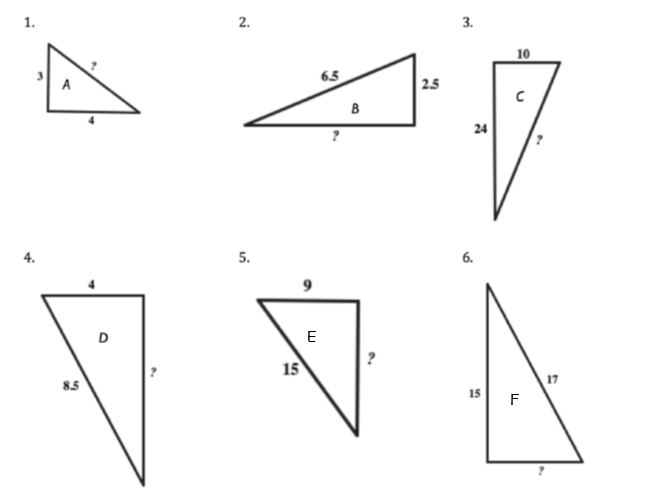
4. For each right triangle below find the missing side n (Pythagorean Theorem could be helpful) and the missing angle, a (Angle Sum Theorem for Triangles could be useful).
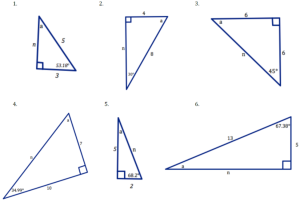
Answer Key:
- a) Yes, b) No
- a) Yes, b) Yes
- 1. 5, 2. 6, 3. 26, 4. 7.5, 5. 12, 6. 8 Triangles A, E; B, C; and D, F are similar.
- 1. 4, 36.82, 2. 7, 60, 3. 8.5, 45, 4. 12, 55.01, 5. 5, 21.8, 6. 12, 22.62
Topic 4: Trigonometric Ratios (4h)
Instructions
- Go through the content and examples with the group, leaving opportunities for questions.
- Have students complete the practice exercises independently, then take up the answers.
Trigonometry is the study of the relationships between the sides and angles of right triangles. The legs are called adjacent or opposite depending on which acute angle is being used.
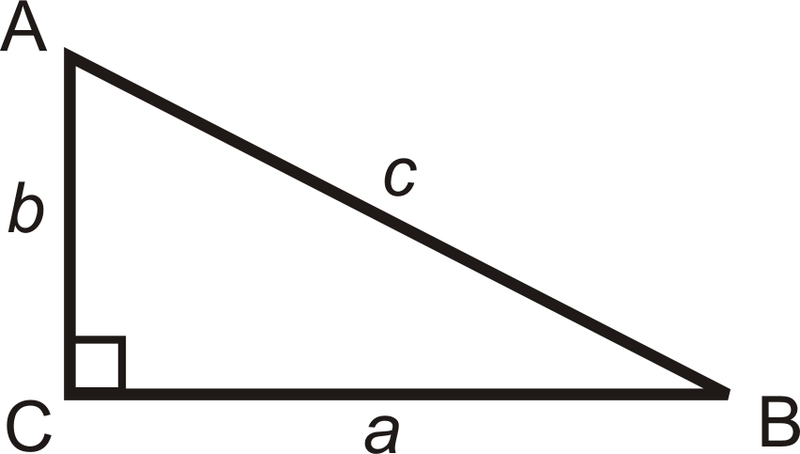
a is adjacent to ∠B
a is opposite ∠A
b is adjacent to ∠A
b is opposite ∠B
c is the hypotenuse
The Hypotenuse is always opposite the right angle. That side should be labeled first. This diagram may help visualize how an angle is labeled.
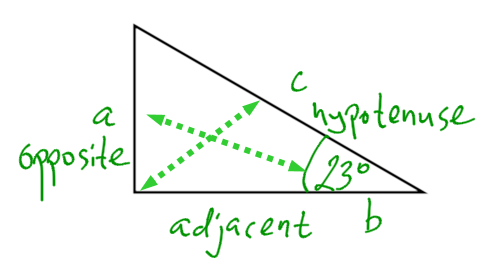
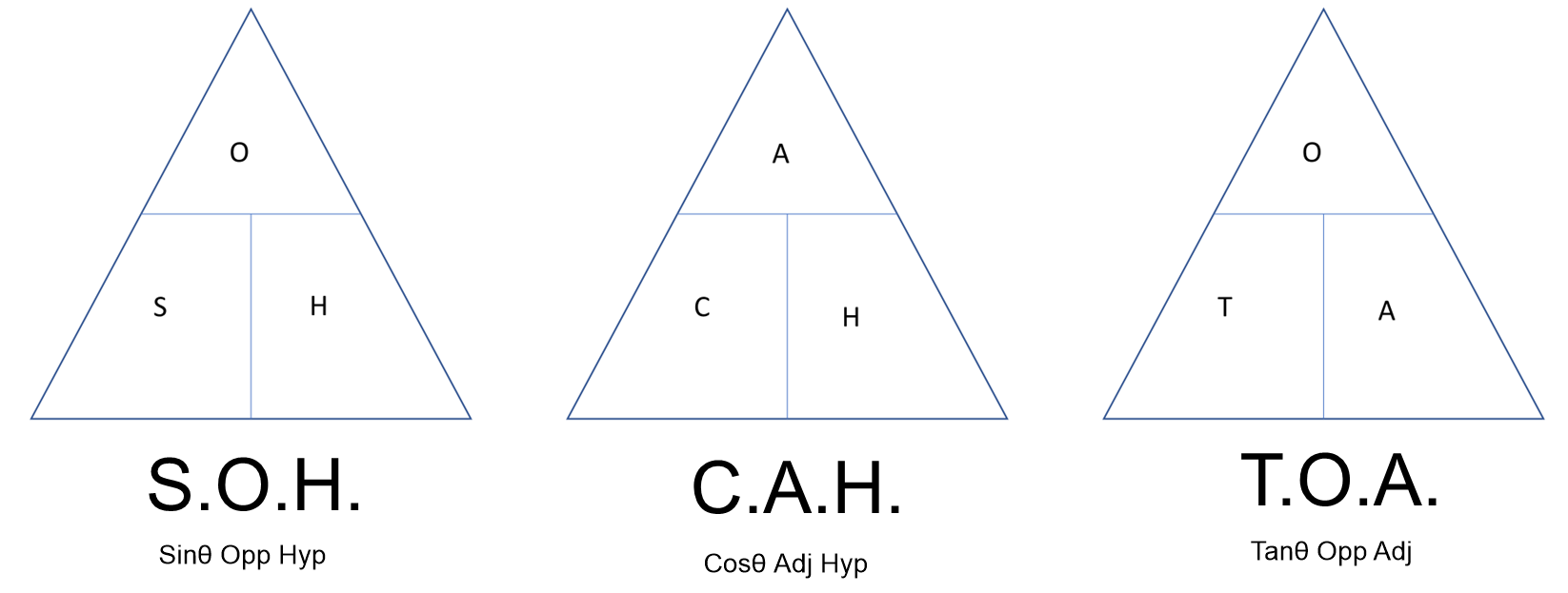
The three basic trigonometric ratios are called sine, cosine and tangent. For right triangle △ABC, we have:
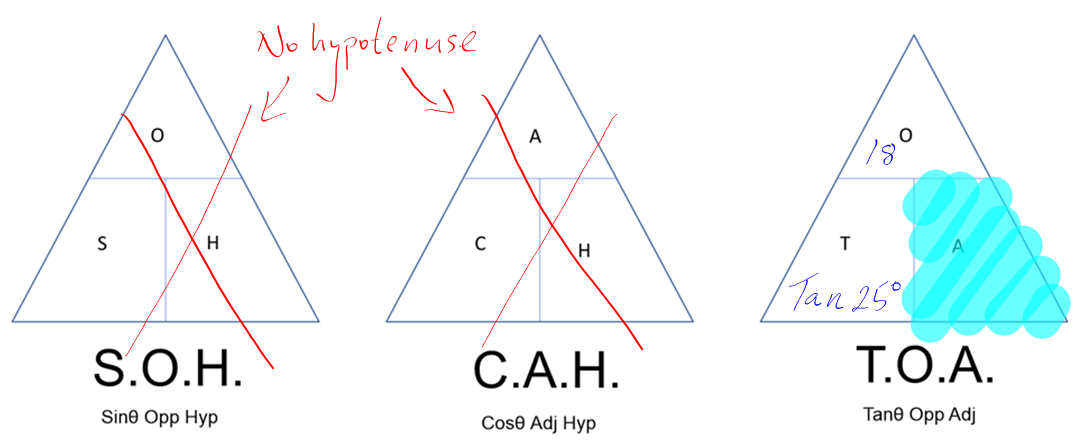
An easy way to remember ratios is to use SOH-CAH-TOA.

Example 1
Find the sine, cosine and tangent ratios of ∠A.
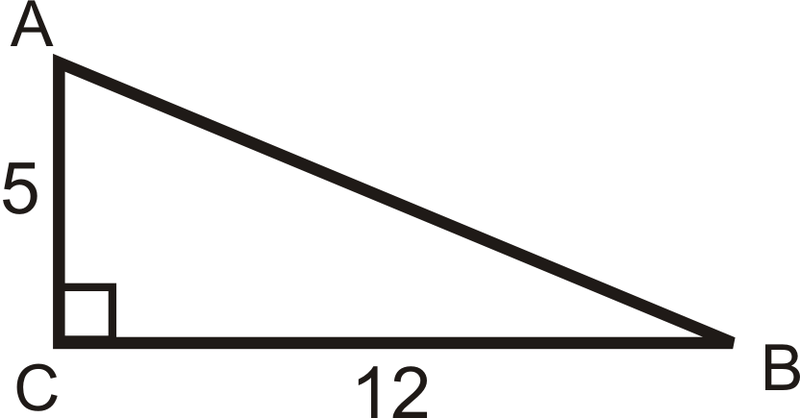
First, we need to use the Pythagorean Theorem to find the length of the hypotenuse.
Example 2
Find the sine, cosine, and tangent of ∠B.
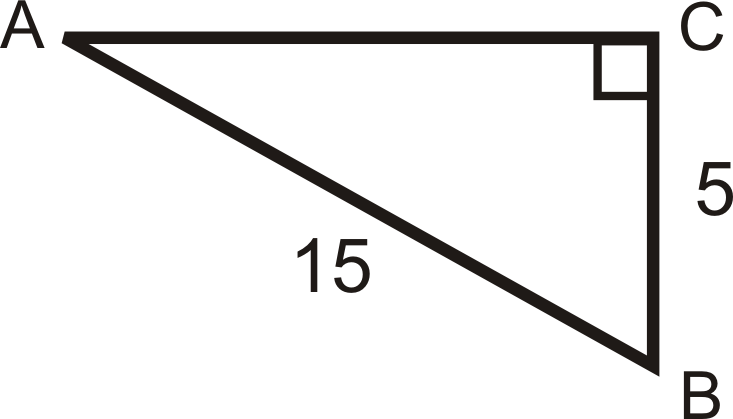
Find the length of the missing side.
Example 3
Find the sine, cosine and tangent of 30∘.
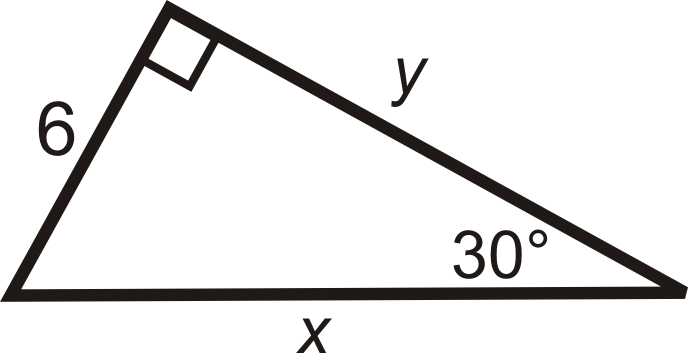
This is a 30-60-90 triangle. The short leg is
Example 4
Answer the questions about the following image. Reduce all fractions.
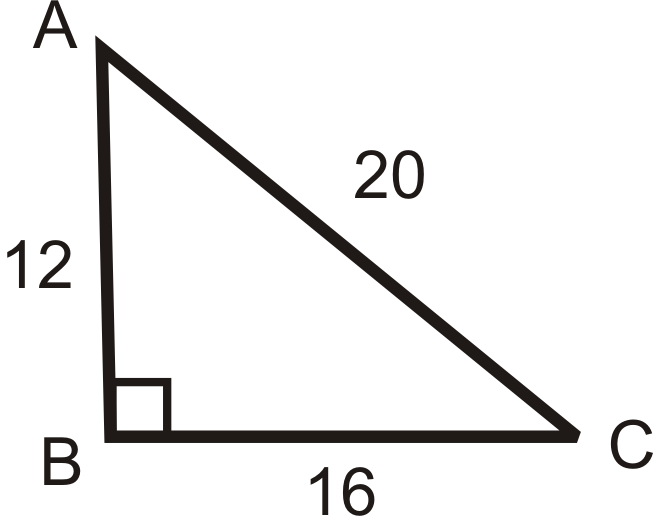
What is sin A, cos A, and tan A?
Optional Activity:
In your notebook draw a right triangle with one angle of 60°.
Measure each side of your triangle as accurately as you can with a centimeter ruler.
Using the 60 degree angle as the angle of reference list the measure for each of the following:
Length of the adjacent side:
Length of the opposite side:
Length of the hypotenuse:
Create the following ratios using your measurements:
Compare your ratios with others that had a triangle of a different size. What do you notice? Explain any connections you find to others’ work?
In the right triangles below find the missing side length and then create the desired ratios based on the angle of reference (angle A and angle D).

List the ratios for ΔABC using angle A as the angle of reference.
List the ratios for ΔDEF using angle D as the angle of reference.
- What do you notice about the ratios from the two given triangles? How do these ratios compare to the ratios from the triangle you made on the previous page?
- What can you infer about the angle measures of ΔABC and ΔDEF
- What can you conclude about the ratio of sides in a right triangle that has a 60° angle? Would you think that right triangles with other angle measures would have similar relationships among their ratios?
Practice Exercises: Pythagoras’ Theorem and the Sum of Angles in a Triangle.
For each right triangle and the identified angle of reference create the desired trigonometric ratios. If any sides of the triangle are missing, find them before determining the ratio.

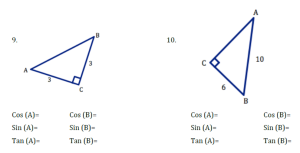
Answer Key:
7. Cos(A)=.496 , Sin(A)=.868 , Tan(A)=1.75, Cos(B)=.868, Sin(B)=.496, Tan(B)=.571
8. Cos(A)=.943, Sin(A).333, Tan(A)=.353, Cos(B)=.333, Sin(B)=.943, Tan(B)=2.833
9. unknown side: 4.2 Cos(A)=.714, Sin(A)=.714, Tan(A)=1, Cos(B)=.714, Sin(B).714, Tan(B)=1
10. unknown side: 8 Cos(A)=.8, Sin(A)=.6, Tan(A)=.75, Cos(B)=.6, Sin(B)=.8, Tan(B)=1.33
Topic 5: Using Trigonometric Ratios to find Sides (4h)
Instructions
- Go through the content and examples with the group, leaving opportunities for questions.
- Have students complete the practice exercises independently, then take up the answers.
The whole point of understanding the trigonometric ratios is that we can use them to find an unknown side or angle in a right angle triangle. (Both Pythagoras’ Theorem and the Trigonometric Ratios only work in right angle triangles.)
There is a strategy to follow for finding the unknown side in a triangle:
- Label the triangle.
- Choose a trigonometric ratio that suits the problem.
- Solve the trigonometric ratio for the unknown side.
- Substitute the numbers in.
- Calculate.
Example
Find the unknown side c.
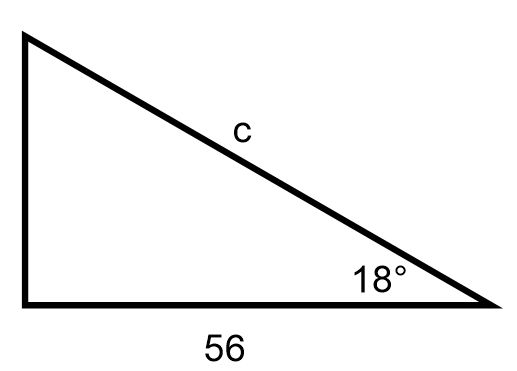
Solution
C is the hypotenuse of the triangle, but we cannot use Pythagoras’ Theorem to find it because there is only one other side known. We can use a trigonometric ratio to solve for the unknown side because this is a right angle triangle.
1. Label the triangle.
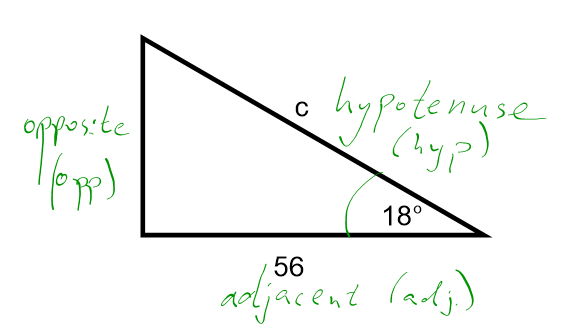
It is often convenient labeling the hypotenuse first, so there is never any confusion between the hypotenuse and the adjacent.
1. Choose a trigonometric ratio that suits the problem. Each equation will require two sides and an angle. You need to know 2 out of 3 variables in the equation to be able to solve for the third.
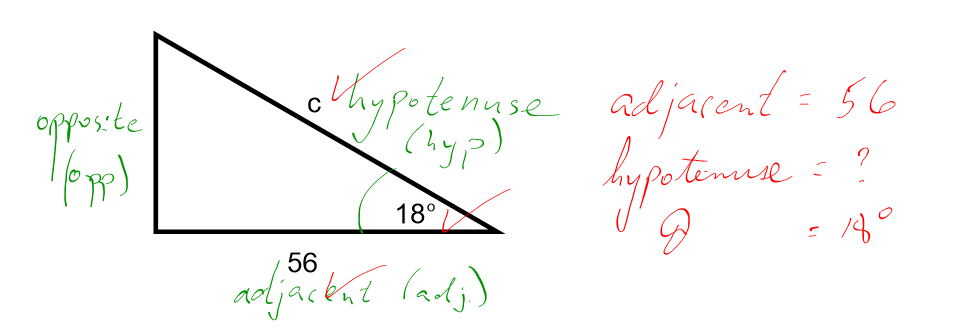
In this case, the opposite is not known and not required to be known. It is out of the picture. Look at the chart below, and determine the ratio that has the angle, the adjacent and the hypotenuse is cosine.

2. Solve the trigonometric ratio for the unknown side. (Hypotenuse)
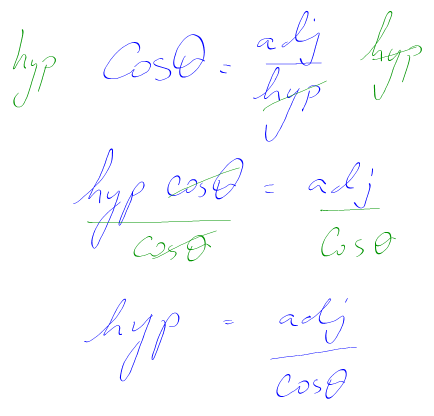
3. Substitute the numbers in.
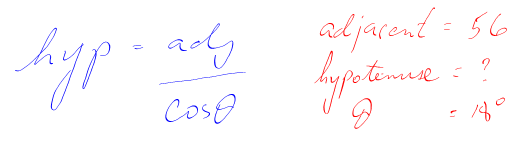
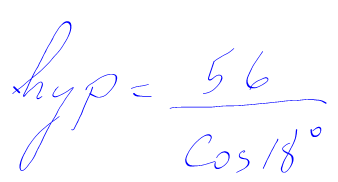
4. Calculate.
Using your calculator:

The unknown hypotenuse is 59.
There is a potentially easier way to accomplish the previous example without using algebra. We can use the tradesperson triangle trick. (This shows up in out PLT Science course.)
Example:
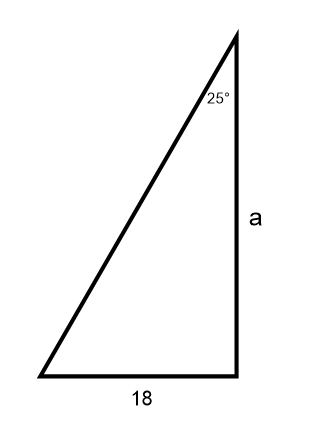
1. Label the Triangle
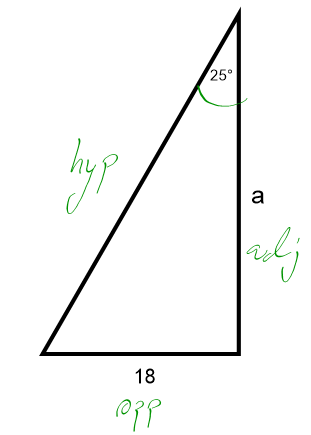
2. Choose the tradesman triangle that has the appropriate values:
3. Calculate:
The triangle above tells us that adjacent is opposite divided by tan 25. (In the triangle the opposite appears above the tan 25.)
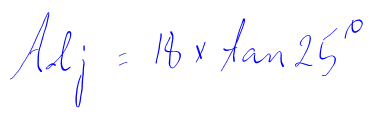
Using the calculator:

The unknown adjacent side is 8.4
Practice Exercises: Using Trigonometric Ratios to find Sides
Solve for the unknown side:
1.
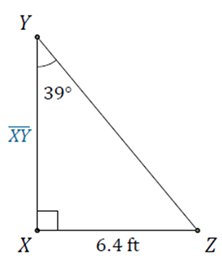
2.
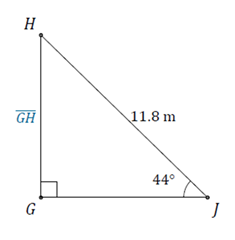
Answer Key:
1. 7.9
2. 8.2
Topic 6: Using Inverse Trigonometric Ratios to find Angles (4h)
Instructions
- Go through the content and examples with the group, leaving opportunities for questions.
- Have students complete the practice exercises independently, then take up the answers.
In mathematics, the word inverse means “undo.” For example, addition and subtraction are inverses of each other because one undoes the other. When we use the inverse trigonometric ratios, we can find acute angle measures as long as we are given two sides.
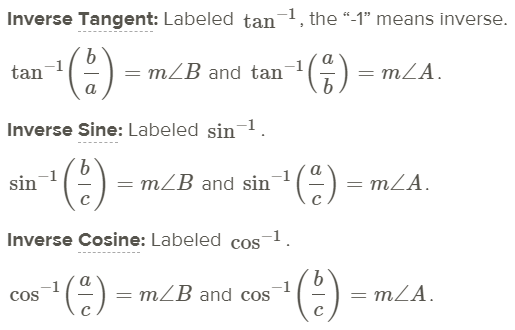
In most problems, to find the measure of the angles you will need to use your calculator. On most scientific and graphing calculators, the buttons look like [SIN−1],[COS−1], and [TAN−1]. You might also have to hit a shift or 2nd button to access these functions.
Now that you know both the trig ratios and the inverse trig ratios you can solve a right triangle. To solve a right triangle, you need to find all sides and angles in it. You will usually use sine, cosine, or tangent; inverse sine, inverse cosine, or inverse tangent; or the Pythagorean Theorem.
Example 1
Solve the right triangle.
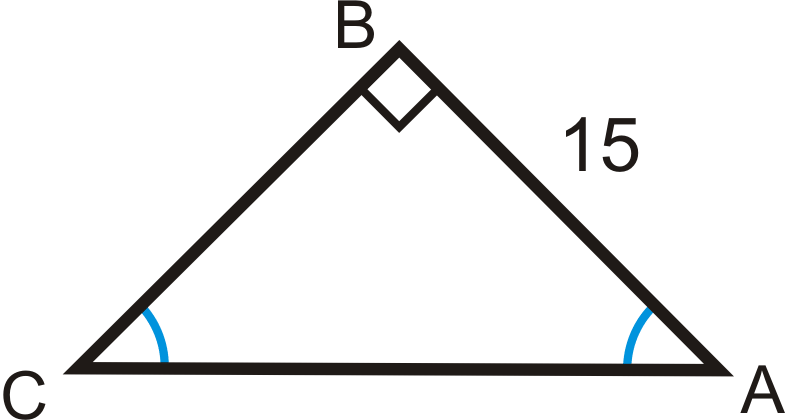
The two acute angles are congruent, making them both 45∘. This is a 45-45-90 triangle. You can use the trigonometric ratios or the special right triangle ratios.
Trigonometric Ratios
Example 2
Use the sides of the triangle and your calculator to find the value of ∠A. Round your answer to the nearest tenth of a degree.
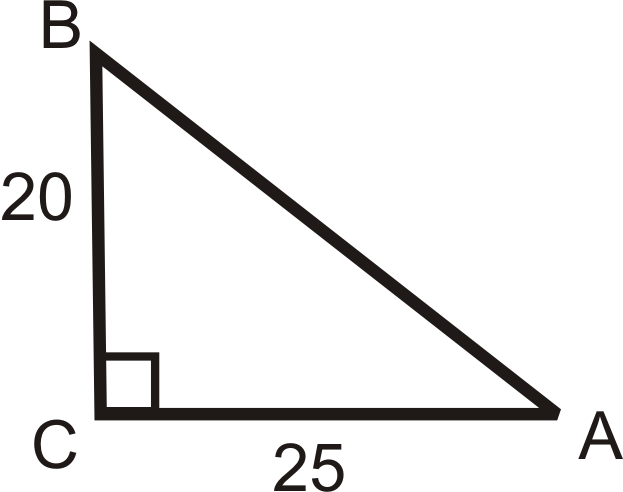 In reference to ∠A, we are given the opposite leg and the adjacent leg. This means we should use the tangent ratio.
In reference to ∠A, we are given the opposite leg and the adjacent leg. This means we should use the tangent ratio.
Example 3
∠A is an acute angle in a right triangle. Find ∠A to the nearest tenth of a degree for sin(A) = 0.68, cos(A) = 0.85, and tan(A) = 0.34.
Example 4
Solve the right triangle.
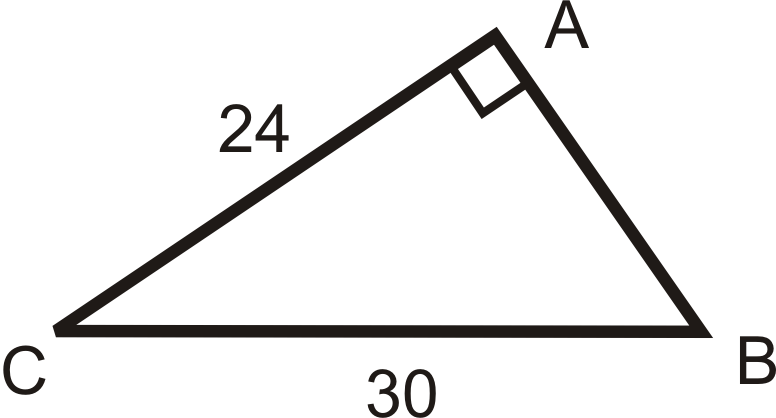
To solve this right triangle, we need to find AB, ∠C and ∠B. Use only the values you are given.
For side AB use the Pythagorean Theorem
For angle B use the inverse SIN ratio
For angle C use the inverse cosine ratio
Example 5
When would you use sin and when would you use sin−1?
You would use sin when you are given an angle and you are solving for a missing side. You would use sin−1 when you are given sides and you are solving for a missing angle.
Practice Exercises: Using Trigonometric Ratios to find Angles
Use your calculator to find angle A to the nearest tenth of a degree.
1. 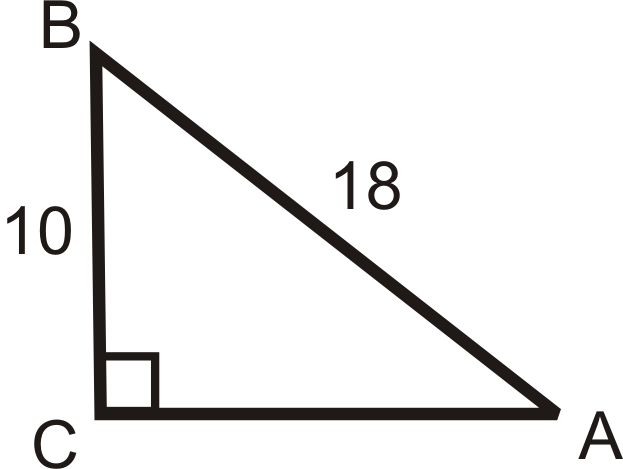 |
2. 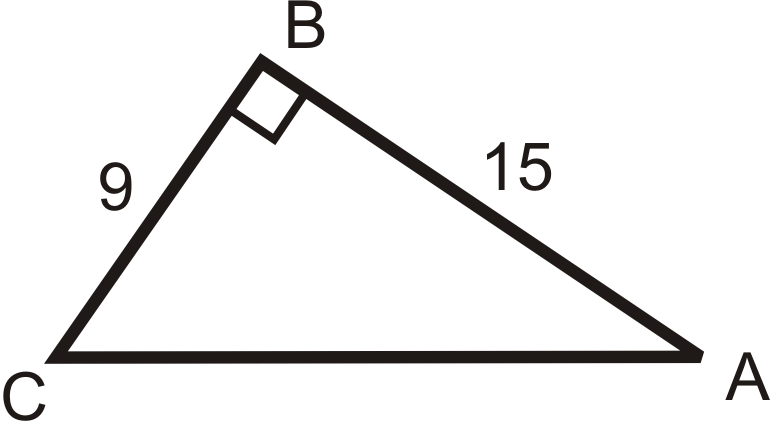 |
3. 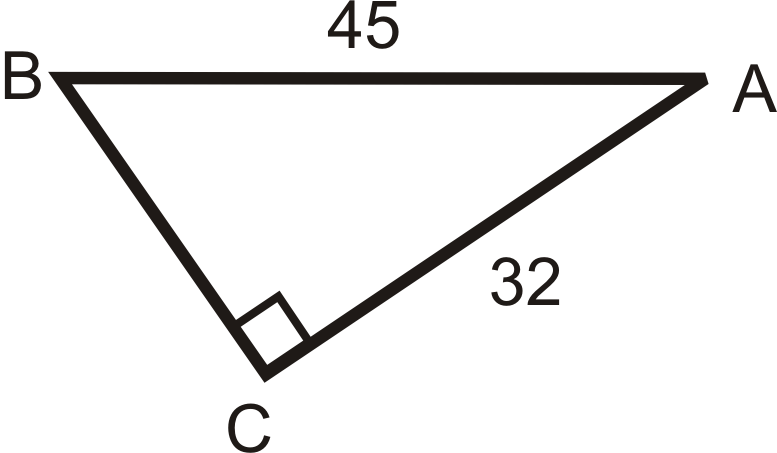 |
4. 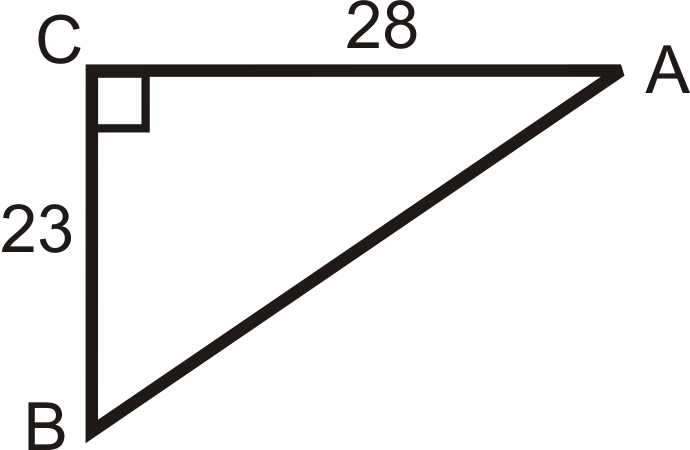 |
5. 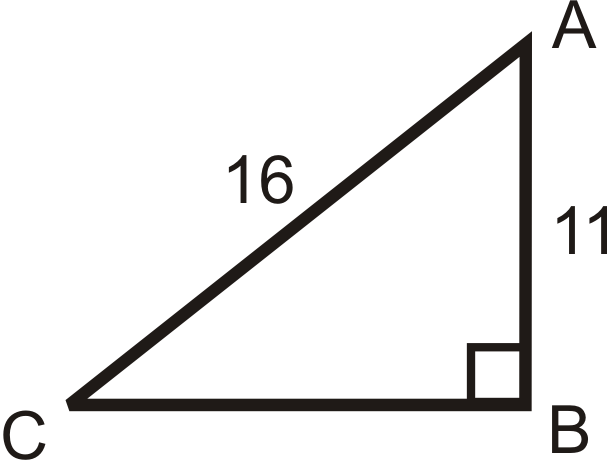 |
6.  |
Let angle A be an acute angle in a right triangle. Find angle A to the nearest tenth of a degree.
- Sin(A) = 0.5684
- Cos(A) = 0.1234
- Tan(A) = 2.78
- cos−1 (0.9845)
- tan−1 (15.93)
- sin−1 (0.7851)
Solve the following right triangles. Find all missing sides and angles. Round any decimal answers to the nearest tenth.
13. 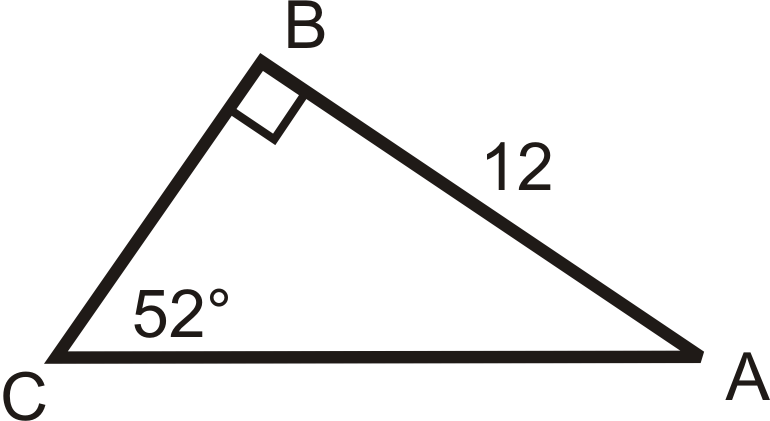 |
14. 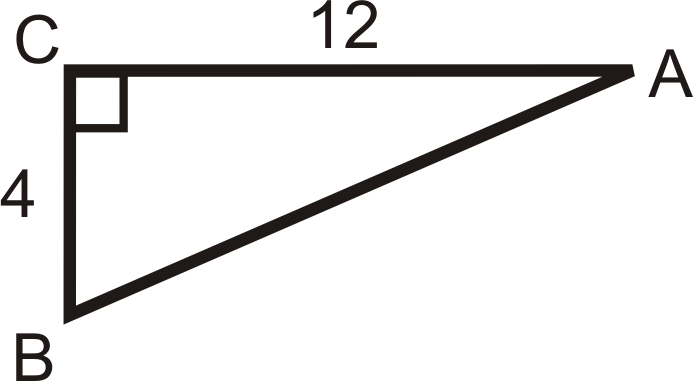 |
15. 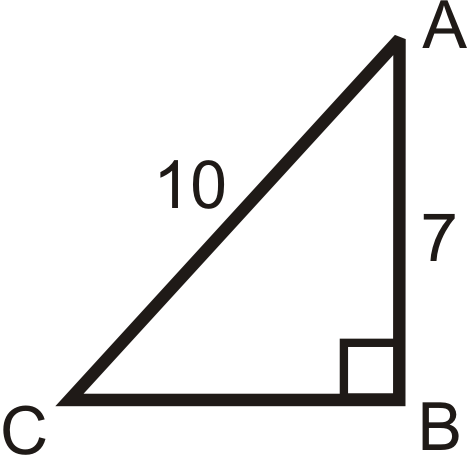 |
16. 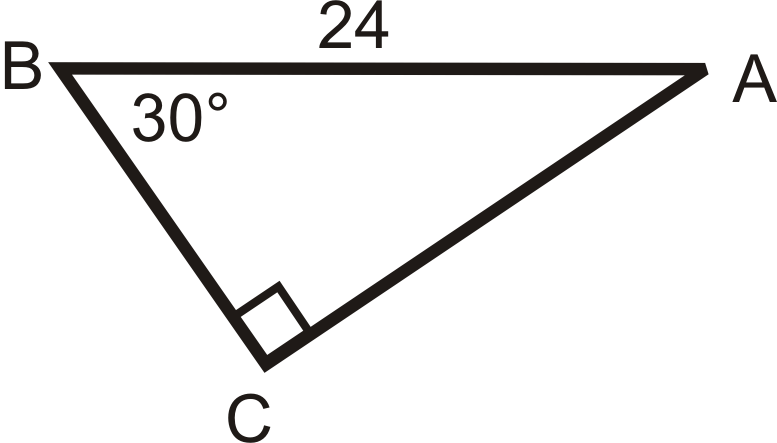 |
17. 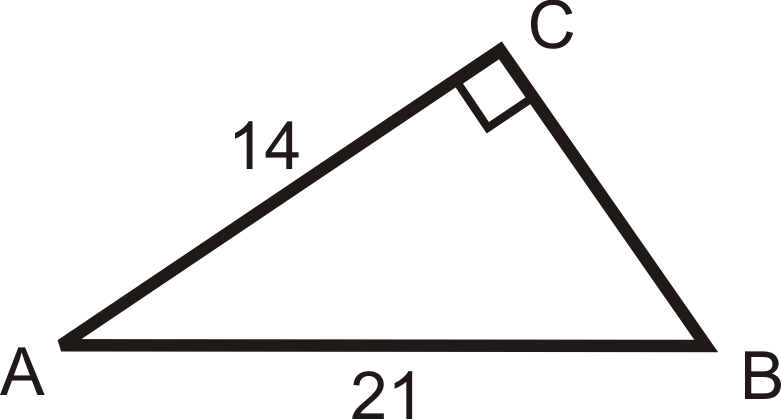 |
18. 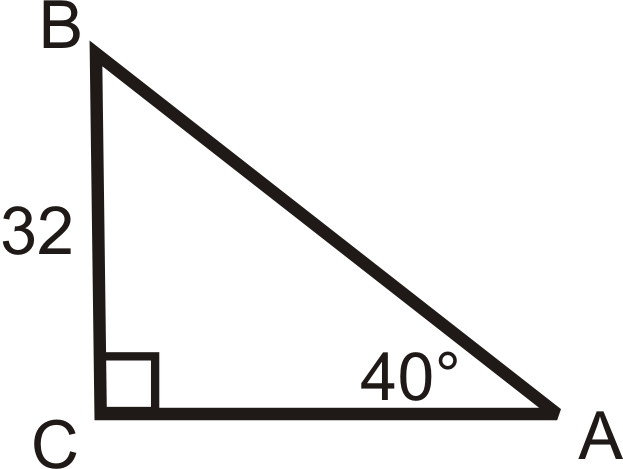 |
19. 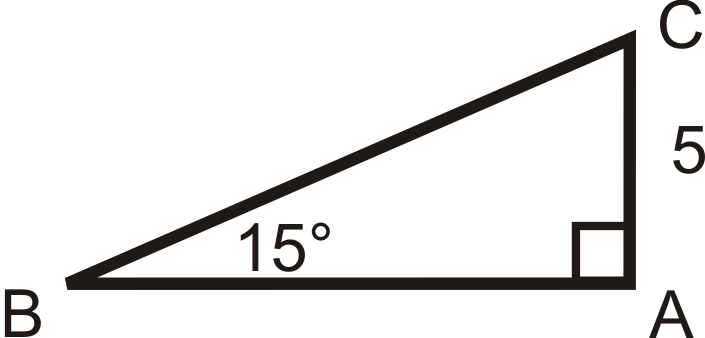 |
20. 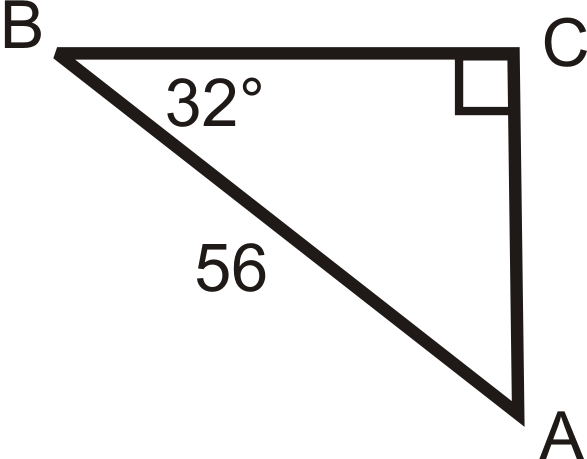 |
21. 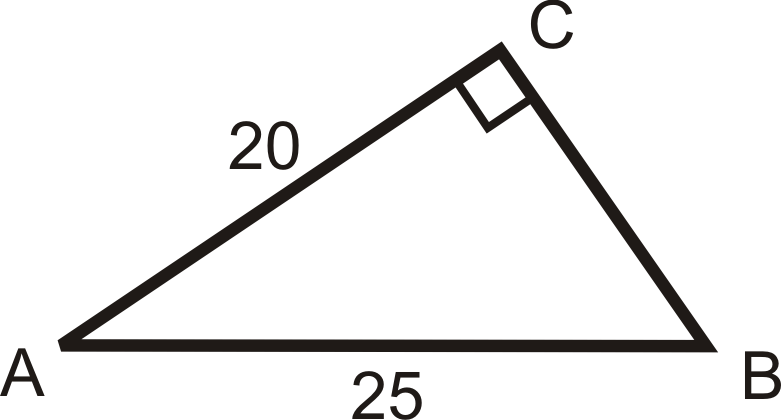 |
Answer Key