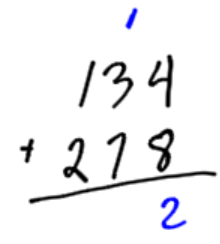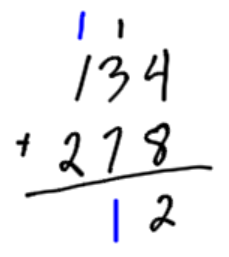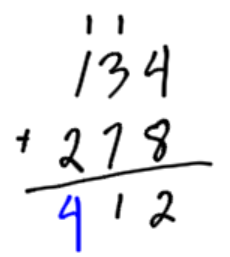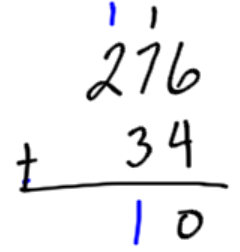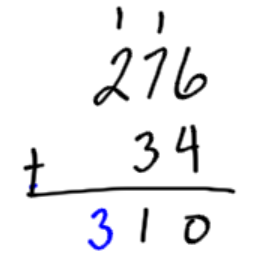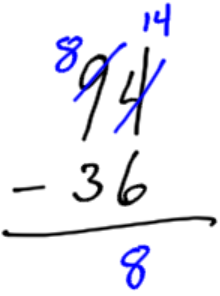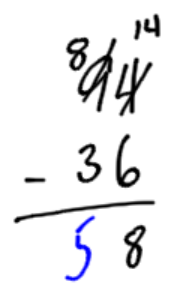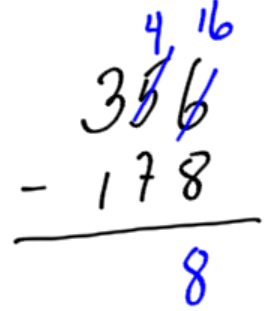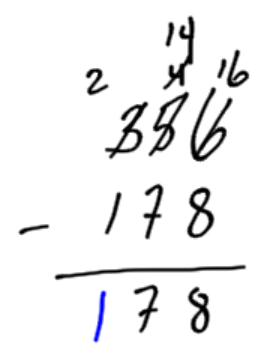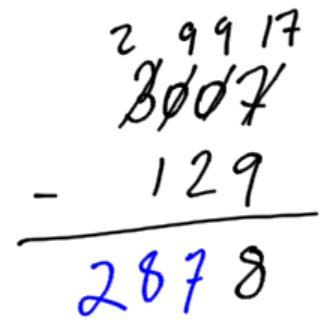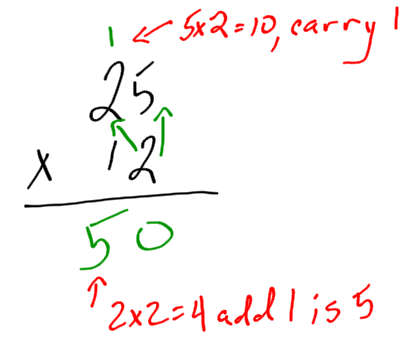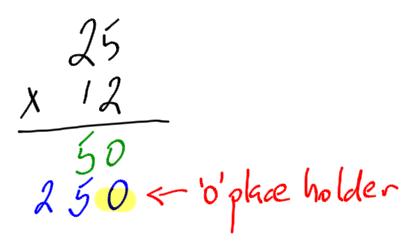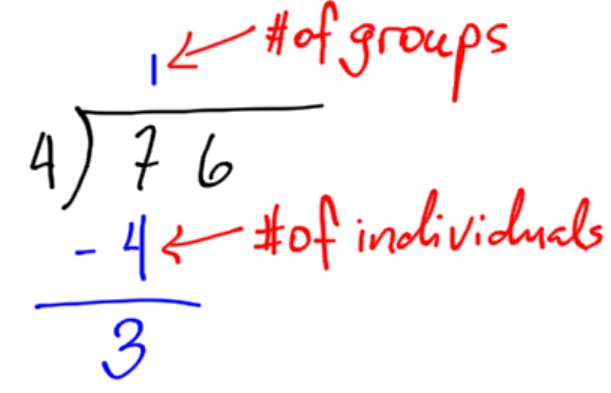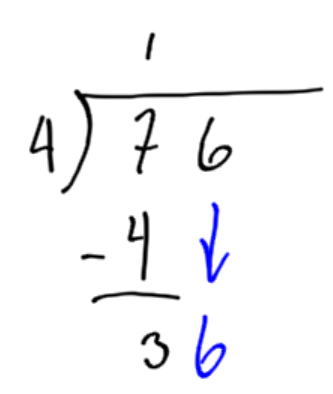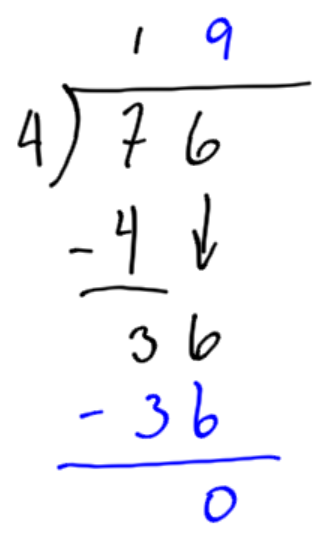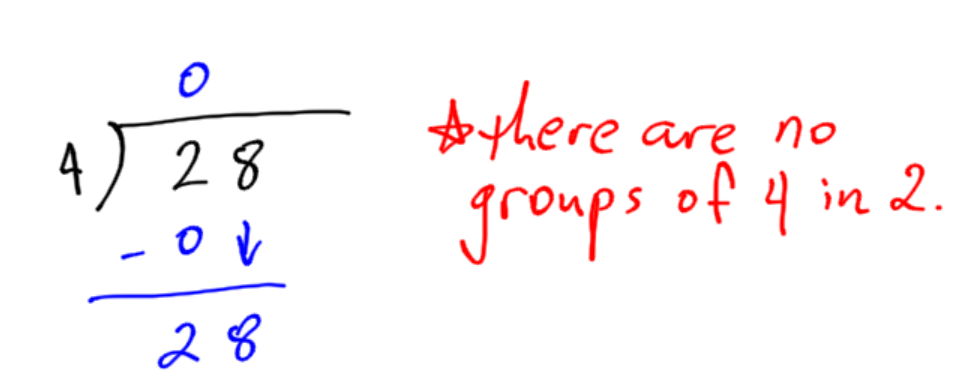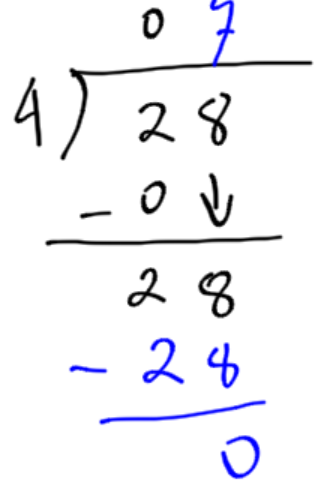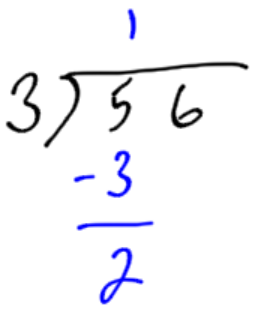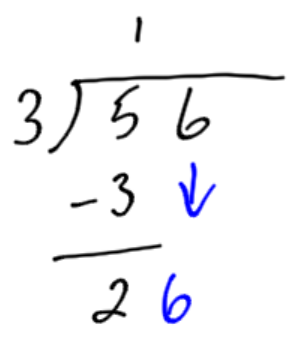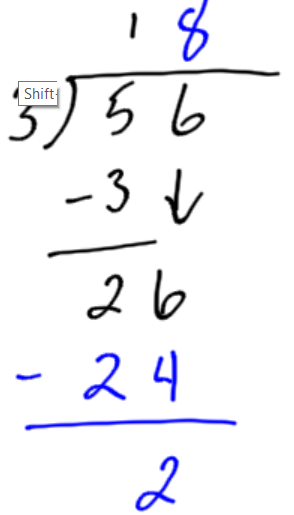1 Basic Operations

In this module you will learn about whole numbers, decimals, rounding, addition, carrying, subtraction, borrowing, long multiplication, long division and order of operations. You will be provided with examples of each concept, and then be given opportunities to practice.

Chapter Contents

Topic 1 Whole Numbers

1.1 Place Value

Topic 2 Decimal Numbers

2.1 Decimals

2.2 What do Decimals Really Mean?

2.3 Whole Numbers and Decimals

2.4 Rounding

Topic 3 Mathematical Operations on Whole Numbers

3.1 Addition and Carrying

3.2 Subtraction and Borrowing

3.2.1 Adding and Subtracting Decimals

3.2.2 Construction Trades Topic: Adding and Subtracting Feet and Inches

3.2.3 Construction Trades Topic: Adding and Subtracting Degrees Minutes Seconds

3.3 Long Multiplication and Carrying

3.4 Long Division

Topic 4 Order of Operations

Test Outcome 1

Topic 1: Whole Numbers

---

Whole numbers are non-negative numbers without fractions or decimals.  An example of whole numbers are 0, 1, 2, 3 and so on.  Negative 30 (-30) degrees celcius is not a whole number.  7.2, or 3/4 are also not whole numbers.

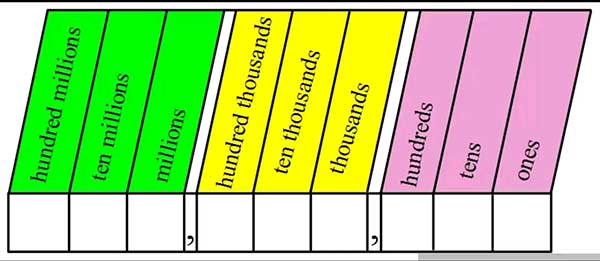
1.1 Place Value

Knowing place value is important when rounding numbers. It will also help us understand why “carrying” and “borrowing” works in addition and subtraction.

If a person has 1 loony, 3 ten-dollar bills, and 2 hundred-dollar bills, we can say that person has $231 (two hundred thirty-five) dollars.

Each digit in a number has a value. The position in the number determines the value. For example, the number “231” is 1 “one” plus 3 “tens” plus 2 “hundreds”.

Here is a chart giving the names of place values:

This Photo by Unknown Author is licensed under CC BY-NC-ND

Example 1

The number 628,134,593 has:

6	Hundred-millions
2	Ten-millions
8	Millions
1	Hundred-thousands
3	Ten-thousands
4	Thousands
5	Hundreds
9	Tens
3	Ones

1.1 Practice Exercises: Whole Number Place Values

Topic 2: Decimal Numbers 

---

2.1 Decimals

It is important to understand what decimals really are because you will come across them every day. Decimals represent a portion (or fraction) of a whole number.

Just like whole numbers have a place value for each digit, decimals also have a place value for each digit. The “decimals” are to the right of the period (decimal point).

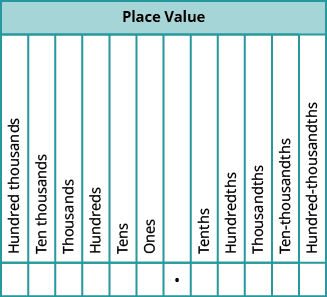This Photo by Unknown Author is licensed under CC BY

NOTE:

• Each decimal place value name ends in -th.
• There are no “oneths”. Decimals start at tenths.

Example 2

The number 0.234 is often read out as “zero point two-three-four.” This is ok; everyone will understand what you are saying. Technically, the number should be read out “two hundred thirty-four thousandths.” By reading it this way, you are saying the last digit in the number is in the thousandth position.

2.1 Practice Exercises: Decimals

 

The Digit Zero Zeros written to the right of the decimal part do not change the value of the number. For example, 95.23 is the same as “95.230”. Zeros written to the left of the whole number part do not change the value of the number. For example, 95.23 is the same as “095.23”. The decimal point is not written after a whole number only for convenience. It still exists. For example, 95 is the same as “95.” or even “95.0”

2.2 What do Decimals Really Mean?

Decimals are fractions and fractions are decimals. We know generally that “one half” is the same as 0.5. Why is this?

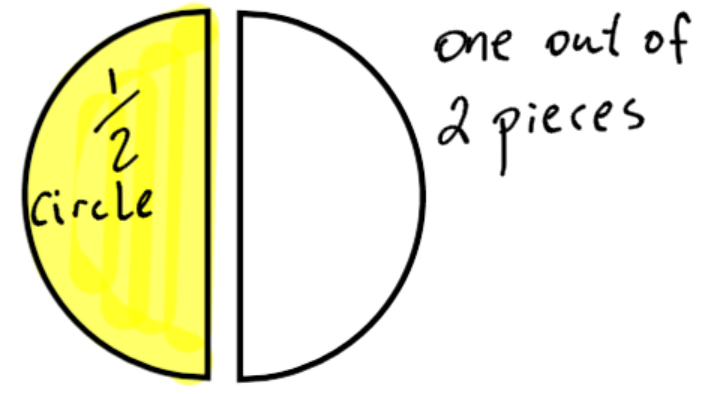
Two pieces represent the whole circle. One piece is 1 out of 2 pieces, also written as ½.

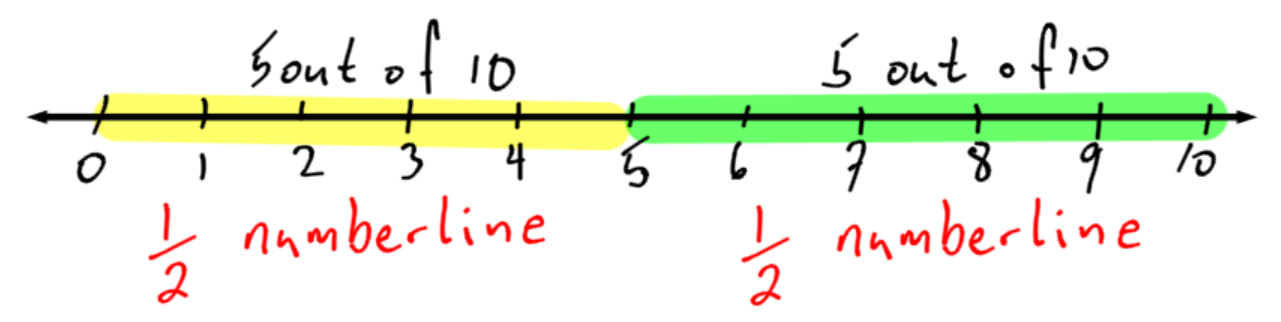
If you divide 10 into two equal pieces, each piece contains 5 numbers. Another way of saying this is “five-tenths.”

As we learned before, “five-tenths” can be written as “0.5”.

Notice the word divide from above. This is a keyword. Check-in your calculator: press 5 ÷ 10. You should see the answer: “0.5”.

In general, the way to change a fraction into a decimal is to use division. (One way to remember this is that the division sign on your calculator ÷ looks like a fraction.)

2.2 Practice Exercises: Converting Fraction to Decimal

2.3 Whole Numbers and Decimals

In the last practice question, you may have noticed that the answer had a “1” to the left of the decimal. Notice also that the top number of the fraction is larger than the bottom number. (11 is larger than 8.) This is called an “improper fraction.”

When the top number of a fraction (numerator) is larger than the bottom number (denominator), the result is more than one. Literally, you have enough pieces to make one whole, with more pieces left over.

Seven quarters is the same as one full piece of pizza with 3 pieces left over (the pieces are quarters.)

We will cover this in greater detail under the topic “Fractions.”

2.4 Rounding

Rounding is an important skill. Whenever you do a calculation with numbers, you have the potential to create a whole bunch of decimals on your calculator. Not only are all these numbers a pain to write down, but they are also meaningless.

A Grain of Sand If, for example, you are calculating the volume of sand going into some concrete, you will need to multiply three numbers together. Sand weighs about 1.6 grams per cubic centimeter. If you calculate the volume of sand to be 2352.000045 centimeters cubed, the weight of that sand will be 3763.200072 grams. If the volume of the sand were to be only 2352 centimeters cubed, the weight of the sand would be 3763.2 grams. The point is, the extra 0.000072 grams of sand is so small, it can’t even be measured by a normal scale. It is less than one grain of sand! So, using all the decimals in 2352.000045 is meaningless.

A number can be rounded off to include any number of decimal places you want.

There are three basic steps to rounding:

• Identify the “round-to” digit
• Look one digit to the right
• Decide to round up to the next “round-to” digit or keep the same “round-to” digit.

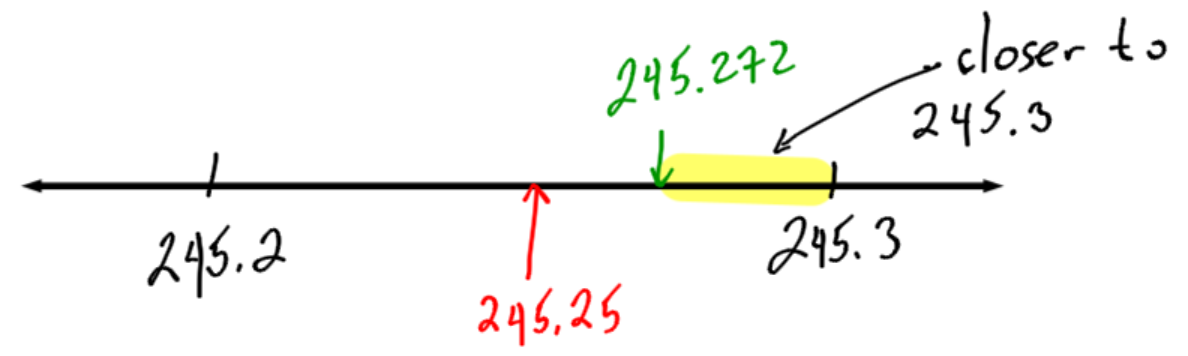
Example 3

Round 245.272 to the nearest tenth.

Step	What I am thinking
Identify the “round to” digit	We are rounding to the nearest tenth. The digit in the tenth’s spot is 2. The final answer will only have one decimal (the tenth) and it will be either 2 or 3 (depending on if we round up or down.)
Look one digit to the right	The digit to the right is 7.
Decide to round down or up	Since the digit to the right is larger than 5, it is more than half-way to 245.3. It is closer to 245.3 than 245.2. We can round up to 245.3

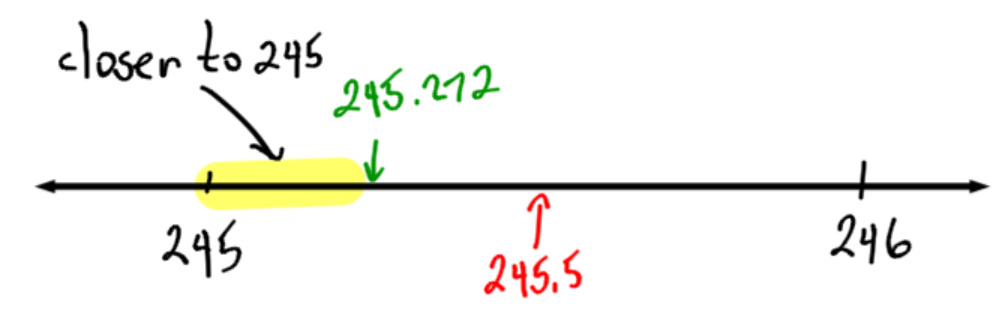
Example 4

Round 245.272 to the nearest whole number (ones).

Step	What I am thinking
Identify the “round to” digit	We are rounding to the nearest whole number (ones.) The digit in the ones spot is 5. The final answer will only have whole numbers and it will be either 5 or 6 (depending on if we round up or down.)
Look one digit to the right	The digit to the right is 2. (It doesn’t matter that it is on the other side of the decimal.)
Decide to round down or up	Since the digit to the right is less than 5, it is less than half-way to 246. It is closer to 245 than 246. We can round down to 245

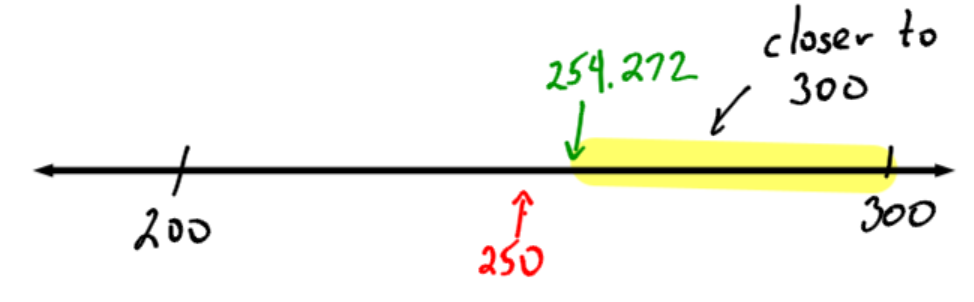
Example 5

Round 254.272 to the nearest hundred.

Step	What I am thinking
Identify the “round to” digit	We are rounding to the nearest hundred. The digit in the hundreds spot is 2. The final answer will only have whole numbers and it will be either 200 or 300 (depending on if we round up or down.)
Look one digit to the right	The digit to the right is 5. (All the rest of the digits to the right of 5 don’t play any part in this.)
Decide to round down or up	Since the digit to the right is 5, the answer could go down to 200 or to up to 300. In this case, I can look one more digit to the right: 254. The number is slightly more than halfway, so I will round up to 300.

2.4 Practice Exercises: Rounding

Round the following numbers to the given place value:

Topic 3: Mathematical Operations on Whole Numbers 

---

The words “Mathematical Operations” mean addition, subtraction, multiplication, and division. In this section you will learn when to use each “operation”, and how to perform the calculations by hand.

In this section, it will be very important to remember that each digit in a number has a different value. For example, the number 523 has 3- ones, 2-tens, and 5-hundreds.

3.1 Addition and Carrying

Addition is the mathematical operation that combines amounts of the same thing. We will see in the fractions section that when adding, you can only add items of the same type. For example, if you have five apples and three oranges, you may have eight fruits, but you certainly do not have eight apples, nor eight oranges.

The word “sum” is sometimes used to mean “add”. For example: “find the sum of 3 and 5” means the same thing as “add 3 and five.”

Carrying

Maybe the easiest way to understand what is happening with carrying is to think about money. In this situation we have only loonies, ten-dollar bills, and hundred-dollar bills.

Let’s add 35 plus 96. We have five loonies plus six loonies which is in total eleven loonies. To not carry so much change, we cash in eleven loonies for one ten-dollar bill, and we have one loony left over.

Because we only can add things of the same type, we add the one ten-dollar bill in with the other ten-dollar bills. We start with three ten-dollar bills plus nine ten-dollar bills plus the one ten-dollar bill we carried over and have in total thirteen ten-dollar bills.

Even though you could think of your answer as 13 ten-dollar bills, and one loonie, you can see there is a 1 is written in the hundered’s spot.  Just like before with the loonies, 10 ten-dollar bills get changed into 1 hundred-dollar bill with three tens remaining.

Example 1

Add the numbers 134 and 278. In this example, we will carry over to the tens spot and to the hundreds spot.

Step	What I am thinking
	Add the loonies. There are 4 and 8, or 12 loonies. We can cash in for a 10 dollar bill. Add the ten, to the other tens in the tens spot.
	Add all the tens together. The 3 and 7, plus the one you cashed in from before. There are a total of 11 tens. Change 10 tens in for a hundred dollar bill.
	Add all the hundreds together. The answer is 412.

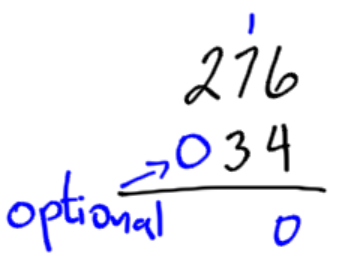
Example 2

Add the numbers 34 and 276. In this example, we usually write the larger number on top, but it is not necessary. Also remember that the number 34 can also be written as 034.

Step	What I am thinking
	Add the 6 loonies and 4 loonies. Change that in for 1 ten dollar bill.
	Add the tens together, including the one you carried over from last step.
	Add the hundreds together including the one from last step. The answer is 310.

3.2 Subtraction and Borrowing

Subtraction is the mathematical operation that finds the space between 2 numbers.

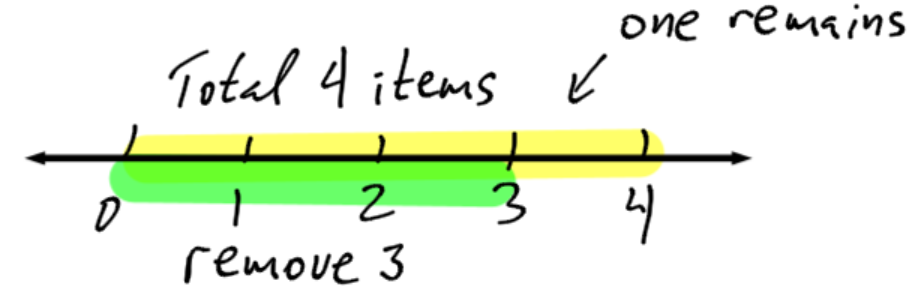
Another way to look at the same thing is to use the number line to count. Start at 4, and count to the left 3 (subtract, or negative, means move left on the number line.)

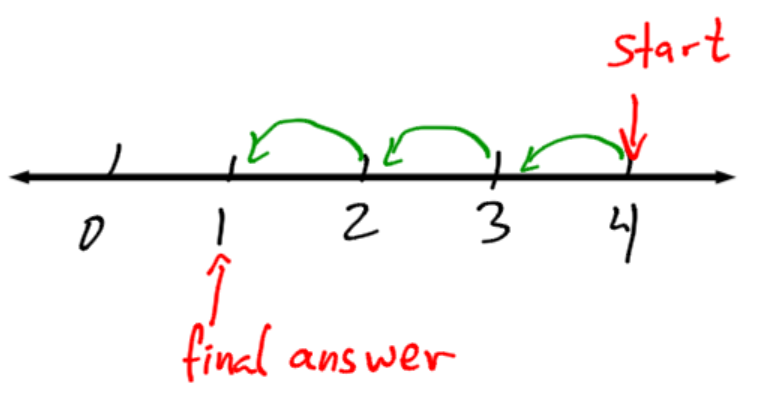
For example, you use subtraction if you give someone money and want to figure out how much you have left. You would also use subtraction if you have used up a certain amount of supplies and you want to see how much you have left.

The word “difference” is sometimes used to mean subtraction, or minus. For example, “find the difference between 32 and 26” means “32 minus 26”. Note the order you subtract numbers in makes a difference. “32 – 26” means something different than “26 – 32.”

Borrowing

Let’s continue thinking about money. We have only loonies, ten-dollar bills, and hundred-dollar bills. when we don’t have enough money to subtract from, we have to take money from another higher place value.

In the previous addition example, we needed to change all our “ones” to “tens.” When borrowing, we need to change “tens” back to “ones.” For example, subtract 36 from 94. (That is written 94 – 36.) If you have 4 loonies, there is not enough to take 6 loonies away. We “borrow” a ten-dollar bill. We need to cash this ten-dollar bill into loonies to be able to give the proper change. I now have 14 loonies (4 originally, and 10 from the 10-dollar bill I borrowed.) 14 loonies subtract 6 loonies is 8 loonies.

Step	What I am thinking
	4 is not large enough to take away 6 from. Borrow 1 ten dollar bill from the 9 (leaving 8). Cash the ten dollar bill in, and add to the four you already have, to make 14. 14 minus 6 is 8.
	Now in the tens spot, there are 8 tens, minus 3 tens leaves 5 tens. The answer is 58.

Example 3

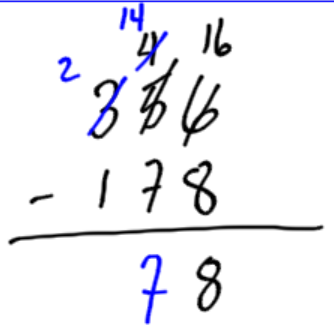
Subtract 178 from 356 (written as 356 – 178.) In this example, we must borrow from the tens, and then again from the hundreds.

Step	What I am thinking
	Six is too small to take eight away. We must take 1 ten from the tens spot. Cash the ten dollar bill into loonies and add it to the 6 loonies you already have. 16 – 8 = 8
	Now look at the tens spot. There are 4 tens, but we are taking away 7. We must borrow a hundred, and cash in for 10 tens. Add the 10 tens to the 4 we already have. 14-7=7
	Finally, we have two hundred dollar bills, and we are taking away one hundred dollar bill. The final answer is 178.

Example 4

Calculate 3007 minus 129. In this example, we need to look further than just one place value to the left to borrow from

Step	What I am thinking
	The 7 is too small to take away 9. We must borrow, but there is nothing to borrow from the tens, nor the hundreds. Start by borrowing a thousand dollar bill. This sets off a chain reaction. Cash the thousand in for 10 hundreds. Borrow a hundred and cash in for 10 tens. Borrow a ten and cash in for 10 ones. Now we can take 9 away from 17.
	Now we have enough on top to do all the other subtractions. I will do them in one step. 9 tens minus two tens are 7 tens. 9 hundred minus 1 hundred is 8 hundreds. 2 thousands minus zero thousands are 2 thousands. The answer is 2878.

3.2.1 Adding and Subtracting Decimals

Adding and subtracting with decimals is mostly the same as with whole numbers.  The one additional rule to remember is to line up the decimals one on top of the other.  Zero’s can be added both before a number and after.

Example:

Add 0.304 + 343.9

The first step is to write the numbers one on top of the other, so the decimals are aligned.

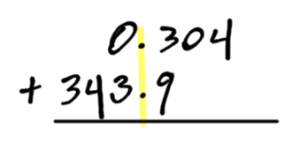
You can add zero’s before and after the numbers if it makes it easier to understand.

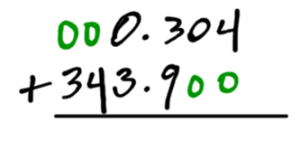
Do the adding as normal.  Keep the decimal in the answer in the same position as above.

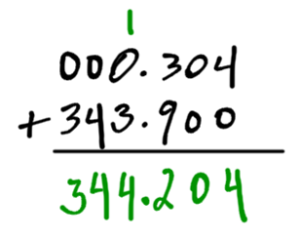
3.2.2 Construction Trades Topic: Adding and Subtracting Feet and Inches

This topic is specific to construction trades and is optional for other programs.

Adding feet and inches is very similar to adding normal numbers but for two exceptions.

• Rather than lining the ones on top of the ones and the tens on top of the tens, and so on, you line the inches on top of the inches and the feet on top of the feet.
• Rather than carrying or borrowing groups of 10, you carry groups of 12. There are 12 inches in one foot.

Example:

Add 3’-2” + 4’-5”.

Note: The dash between the feet and inches is not a subtraction.  It is only a separator between feet and inches.

Feet must be added to feet, and inches must be added to inches.  You can use an upside down “T” to organize your work if you like.

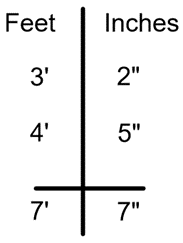
Example:

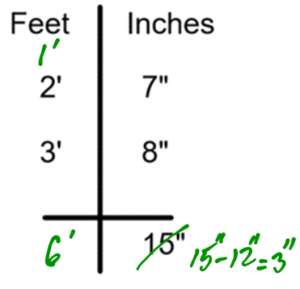
Add 2’-7” + 3’-8”

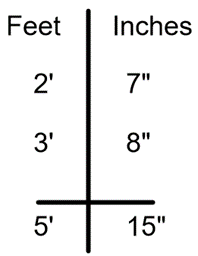
It is not acceptable to write down 15 inches, because within 15 inches, there is one full foot.  In this case, we will need to carry a group of 12 inches (one foot) to the feet column.  As a result, your final answer will be 6’ – 3”.

Example:

Subtract 7’-2” – 2’-9”

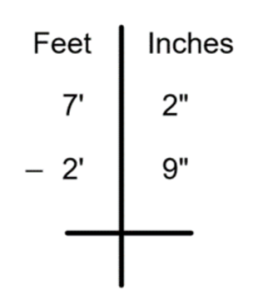
In this case, you cannot take 9 inches away from two.  You need to borrow from the feet.  If you borrow 1 foot, it is changed into 12 inches in the inches’ column.  Add the 12 borrowed inches to the two existing inches to get 14 total inches.  14 minus 9 is 5.

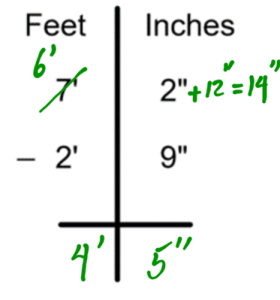
Practice

3.2.3 Construction Trades Topic: Adding and Subtracting Degrees Minutes Seconds

 

This is an extension topic for construction trades and optional for other programs.

In previous sections we have seen that adding and subtracting regular numbers, we cary and borrow in groups of 10.  Adding and subtracting feet and inches requires carrying and borrowing in groups of 12.  In this case, we are going to carry and borrow in groups of 60.

Degrees can be broken down into decimal degrees (such as 32.5^o or “thirty two point five degrees.”)  Another way that is traditionally used to break down degrees is into degrees, minutes, and seconds.  There are 60 minutes in one degree, so 32.5^o in this system would be written as 32^o 30′ (stated thirty two degrees and thirty minutes.)  (0.5 is a half a degree.  If there are 60 minutes in one degree, half of 60 minutes is 30 minutes.)

Example:

32 degrees, 30 minutes, and 45 seconds is written as:

32^o 30′ 45″

Note: the ‘ symbol can be confused with feet.  In the context of degrees, it represents minutes.

Note: the ” symbol can be confused with inches.  In the context of angles, it represents seconds.

Example:

Add 45^o 15′ 25″ + 16^o 50′ 46″

In order to organize the numbers, you can draw collumns as with adding feet and inches.

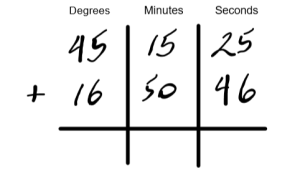
Start by adding the seconds normally, as you would by carrying tens.

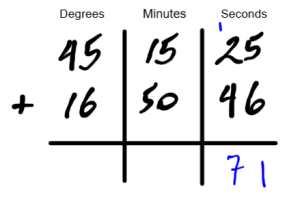
The answer is 71 seconds.  This is larger than one minute (60 seconds).  Cary the one minute into the minutes column and write the remaining seconds in the seconds column.  Add the minutes as normal including the minute you carried over.

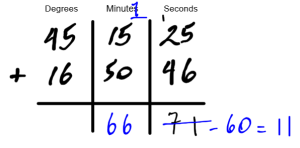
There are more than 60 minutes, so cary one complete degree into the degrees column.  Write the remaining minutes in the minutes column.

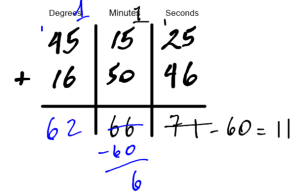
Add the degrees as you would by carrying a group of 10.  Don’t forget to add the degree you carried over from the minutes. The answer is 62^o 6′ 11″.

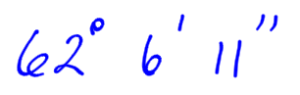
Subtracting is a similar process.  Borrow groups of 60 from the column to the left.

Using the calculator

The TI-30Xa calculator has a function to convert Degree Minute Second (DMS) to decimal degrees, and decimal degrees to DMS.

Example

Enter the angle 32^o 16′ 23″ into the calculator.

Entering an angle looks like entering a decimal, but it is not.  Enter:

32.1623

This tells the calculator that what looks like a decimal is actually degree minutes seconds.

Note: if there are 0 minutes or seconds, you must enter ’00’.  For example 32^o 27″ must be entered as 32.0027.

Example

Add the angles: 32^o 16′ 23″ + 17^o 12′ 19″

Enter into the calculator:

32.1623 + 17.1219 =

The answer will appear as:

3.3 Long Multiplication and Carrying

Multiplication has to do with groups of things. For example, if you have five boxes, and each box contains six things, in total you have thirty things. You could come up with this answer by adding six- five times: 6 + 6 + 6 + 6 + 6 = 30. An easier way to do this is to multiply: 6 X 5 = 30. Basically, multiplication is a shortcut for adding.

You can note that the order of multiplying numbers does not matter: 6 X 5 = 30 and 5 X 6 = 30.

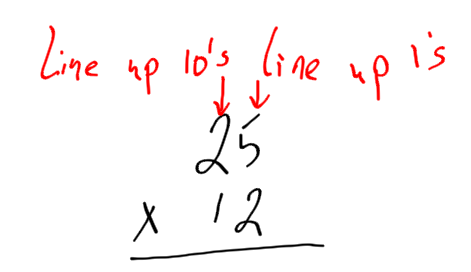
The Process of Long Multiplication

There are steps for doing long multiplication (for example 25 X 12.) In this series of steps, you need to multiply every combination of numbers. Also, the steps may involve carrying, just like in addition.

Let’s walk through this for 25 X 12.

Step	What I am thinking
1. Write the numbers one on top of the other. Put the larger number on top. Line up the ones on top of the ones, tens on top of the tens…
2. Multiply the bottom number by all the top numbers. Carry if necessary. If there is a carried number, add it in after multiplying.
3. Move to the tens. Multiply the bottom number (tens spot) by all the top numbers. Put a “0” place holder because you are multiplying by 10, not 1.
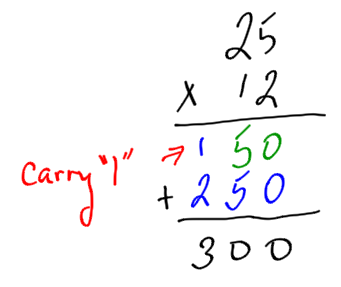
4. Add all the numbers together, using carrying if necessary.

Example 5

Calculate 236 X 129. In this example, we need to multiply ones, tens, and hundreds. There will be three lines to add. Remember the second line has a “0” placeholder. The third line will have a “00” place holder. Here is the work:

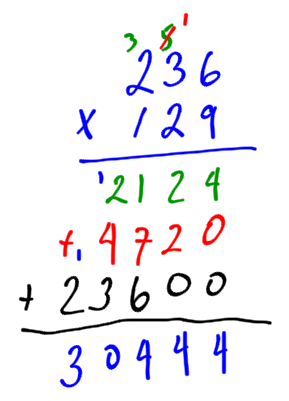
Example 6

An inch can be divided into 8 parts. Each part is called “one eighth”. How many “eighths” are there in 47 inches?

We could add 8 + 8 + 8 + … (47 more times) but this is tedious. Instead, we can use multiplication.

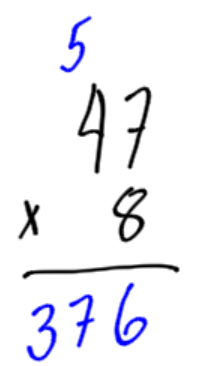
Different Cultures Think Differently The way we have done multiplication is the way we were taught in school. Remember, this is just a procedure that is followed, handed down to use from the European culture. Different cultures have different ways of understanding multiplication. The result is the same: we are adding up groups of numbers. In Asian cultures long multiplication is done completely differently because Asian cultures do not have numbers like Europeans.

Example 7

Using the line method, calculate 53 X 12

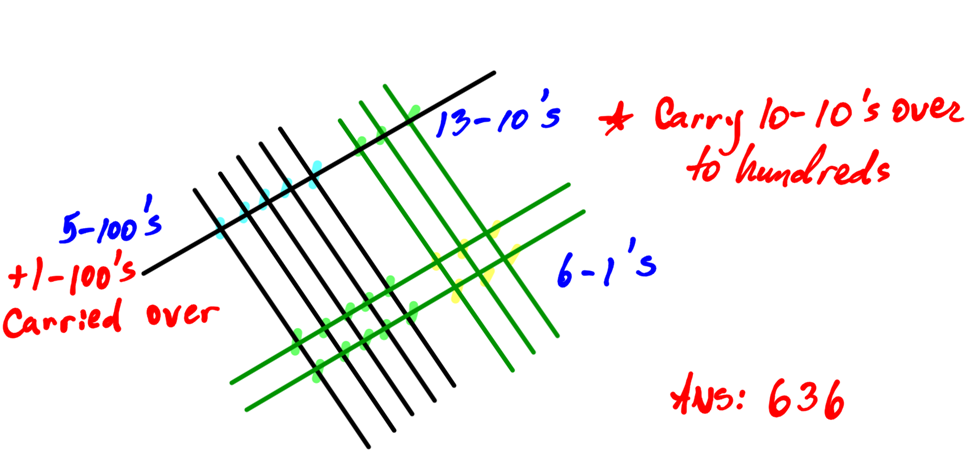
This method requires counting the intersections. The green lines are ones. The black lines are tens.

• Green cross green represents 1 x 1. There are 6 of these intersections.
• Green cross black represents 1 x 10. There are 13 of these intersections.
• The black cross black represents 10 x 10. There are 5 of these intersections.

This means there are 5- ones, 13- tens, and 6- hundreds. We still need to carry 10- tens: change them into 1-hundred and add to the 5 other hundreds.

Then answer is 636.

3.4 Long Division

Long division, in a way, is the opposite of multiplication. Remember, in multiplication, we are figuring out how many individual items there are in a bunch of groups. In division, we are finding out how many groups there are if we collect up items into bunches.

It is important to note that the order of the numbers when dividing matter (unlike multiplication.) There are also many ways of writing division. The words “12 divided by 4” can be typed into your calculator as “12 ÷ 4” or stated as “4 divided into 12” and written like “4 ⟌12”. Also, a division can be represented as a fraction:

You would use division if you wanted to break items up into groups and see how many groups there are.

Just like multiplication, division follows a series of steps that are repeated. Some of these steps may involve borrowing, just like subtraction.

Let’s walk through this for 76 divided by 4.

Step	What I am thinking
	When writing 76 divided by 4 for long division, the 4 goes on the outside. Ask myself: How many groups of 4 are there in 7? There is 1 group of 4, with 3 left over. Write the 1 on top of the 7. Subtract to find the difference of 3.
	Bring the next digit down and put it beside the leftover from the previous step.
	Now we need to find out how many groups of 4 are there in 36. Well, 4 x 9 is 36, so there are nine complete groups of four in 36. There are no more numbers to divide, so the answer is 19.

Example 8

Calculate 28 divided by 4. In this example, we can see what happens when the first number is too small to divide into.

Step	What I am thinking
	Two is not big enough to have any groups of 4. Put a 0 down because there are no groups of 4. Bring down the 8 as before. *Note: you can skip over this step when you realize the first digit is too small.
	There are 7 groups of 4 in 28 (4 x 7 = 28). Write the 7 above the eight. Subtract the answer to find the left over difference. In this case, there is no left over difference.

Example 9

Calculate 56 divided by 3. In this example we can see what happens when a number does not exactly divide evenly into another. We get a remainder.

Step	What I am thinking
	There is one group of 3 in 5, with 2 left over.
	Bring down the 6 to create the next number to divide: 26
	8 groups of 3 items are 24 items. We have 26 items, so there will be two leftover items not in a group. The answer is 18, remainder 2.

Practice Exercises 3.1 – 3.4: Mathematical Operations on Whole Numbers and Decimals

1. What mathematical operation (add, subtract, multiply, divide) would you use in these situations:
   1. You have 90 m between poles and 56 poles. How many meters of the line do you need?
   2. There are 180 degrees total in a triangle. Two of the angles combined are 112 degrees. How many degrees is the third angle?
   3. There is a spool of 1000 m of cable. The space between poles is 90 m. How many poles will one spool of cable cover?
2. Do the following by hand. Check your answer with your calculator.
   1. 1982 + 2399
   2. 3402 – 1929
   3. 2345 X 188
   4. 167 ÷ 12
3. Additional Practice

1 6783 4793 + 6329

2 7403 + 4932

3 67208 + 56256

4 49973 2670 + 367

5 75037 + 56200

• Subtraction:

6 670943 – 569340

7 50376 – 36455

8 67034 – 43578

9 734 – 67

10 3490 – 1678

• Multiplication:

674 × 340

7893 × 38

2001 × 78

734 × 167

28 × 46

• Division: give the answer with the remainder.

180 ÷ 90

894 ÷ 6

6739 ÷ 45

256 ÷ 8

400 ÷ 145

3.1 – 3.4 Practice Exercises Solutions: 

1a. Multiply. 4950, b. Subtract. 68, c. divide. 12. 2a. 4381, b. 1473, c. 440860, d. 13 remainder 11

Note: for 1a and 1c, the first pole is at 0 metres.

-Answers for addition, subtraction, and multiplication not given- check with a calculator.

5. Division: 16. 2; 17. 149; 18. 149 remainder 34; 19. 32; 20. 2 remainder 110

3.5 Exponents

Exponents are important when calculating:

• The total area (if you want to find the number of sheets of drywall necessary, or ceiling tiles, or floor tiles)
• The total volume (if you want to find the total amount of concrete to order for foundation work.)

An exponent means the number of times you multiply a number by itself.

Example:

While it is possible to multiply the individual numbers out on your calculator, there is a shortcut for exponents of 2 (squared) and exponents of 3 (cubed) because these are the exponents used for calculating area, and volume.

Notice the  button.  In order to calculate  as in the example above, press “6”, then the  button.  The answer immediately returns as 36 (no need to press the “equals” button.

In order to calculate  as in the example above:

• Press “2”
• Press the second function button
• Press the “1” button.   (Notice how there is a green on top of the 1.  When you press the second function, the next button does what is written on top in green.)
• The answer immediately returns as 8.

Practice:

Calculate the following exponents:

1. 32 “squared” (written as 32²)
2. 5 “cubed” (written as 5³)
3. 18²
4. 19³

Answers

1. 1024, 2. 125, 3. 324, 4. 6859

Topic 4: Order of Operations

---

In some mathematical calculations, you will need to do several operations in a row to come up with the answer. There is a proper order to do these in. This is called the “order of operations.” (Remember the word “operations” means add, subtract, multiply, or divide.) You may have heard of the term “P. E. D. M. A. S.” or “B. E. D. M. A. S.” This is a way to remember what order to do the operations in. Another way to remember the order of operations is the phrase “Please Excuse My Dear Aunt Sally.”

When doing these questions, do them in multiple steps. In each step, complete one set of operations. Write each step on a new line. Then, compare your answer with an answer obtained with your calculator.

Example 1

Calculate 6 + 7 x 2 using the order of operations.

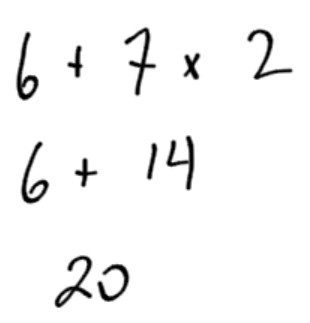
Example 2

Calculate (6 + 7) x 2 using the order of operations.

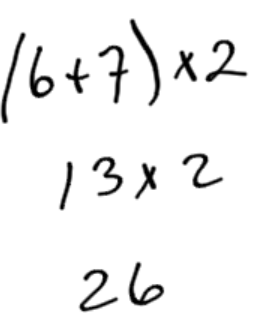
Example 3

Calculate 11 – 3 x 3 + 4 x 2 using the order of operations.

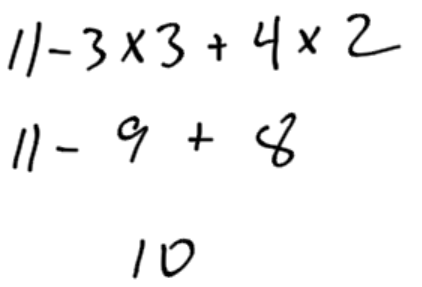
Example 4

Calculate 3 + 2² x 5 using the order of operations.

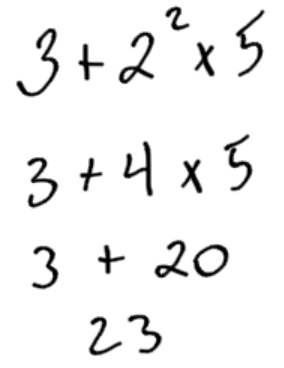
Example 5

Calculate (4 + 1)² + 3 x 2 using the order of operations.

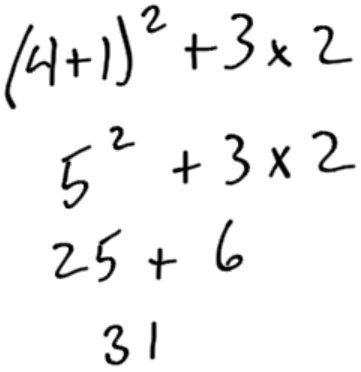
Practice Exercises 4.1: Order of Operations

 

4.1 Practice Exercises Solutions (step-by-step):

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9.