15 Lesson 5
Izabela Mazur and Kim Moshenko

Learning Objectives
By the end of this section it is expected that you will be able to:
- Determine the simple interest earned on an investment or charged on a loan
- Determine the principal amount, the interest rate, or the time for applications involving simple interest
- Determine the maturity value of a loan that involves simple interest
Interest
Some people keep money at home in an easily accessible location, perhaps a piggy bank, a safe or locked box, or perhaps even a mattress. Although this provides instant access to funds it does not provide any return or earnings on this money. For that reason, most people hold their money in accounts or investments that provide some form of return or earning power.
Interest is the price paid for the use of money. If you borrow money from another person or a lending institution, eventually you must pay back this amount plus the interest owing. When you deposit money in a bank, you are lending them money and after some time they will pay you interest on the money you lent them.
The amount of interest you will owe or receive is determined by the principal, the interest rate, and the time (the length of the loan). The amount of money that you lend or borrow is called the principal. The length of the loan can range between a few days to several years. The interest rate is stated as an annual percentage. It may be simple interest or compound interest. With simple interest the interest is calculated only once during the entire time period of the loan or deposit. Simple interest is calculated solely on the principal investment or loan. With compound interest the interest is calculated more than once during the time period of the loan. It will be calculated on the principal as well as the accumulated interest This section will focus on simple interest and in the next section we will consider compound interest.
Simple Interest
Simple interest is calculated by finding the product of the principal (P), the rate (r), and the time (t).
Simple Interest
The simple interest formula is I = Prt where
I = interest earned r = annual interest rate ( stated as a decimal)
P = principal t = time (in years)
Interest rates are quoted for periods of one year and when used in a formula must be converted to a decimal fraction. The time must be expressed in the same unit of time as the interest rate so time must be stated in years or portions of a year. If you deposit money in a savings account earning 3% interest then the annual interest rate is 3% per year.
EXAMPLE 1
Jo borrows $2000 at an interest rate of 5% per year. How much interest will Jo owe after one year?
Solution
Identify the P, r, and t. P = $2000 r = 5% = 0.05 t = 1 year
| Here, | |||
| Replace P, r and t with their values | |||
| Change 5% to its decimal equivalent, 0.05 | |||
Start with the formula I = Prt
I = 2000 (5%) (1) Replace P, r, and t with their values
I = 2000 (0.05) (1) Change 5% to its decimal equivalent, 0.05
I = 100
Jo will pay $100 in interest.
TRY IT 1
Terri borrowed $3200 at an interest rate of 4.75%. How much interest will Terri owe on the loan at the end of one year?
Show answer
![]()
Terri will owe $152 after one year.
Note that the time t is expressed in terms of years. When the time period is not exactly one year, the value for t will be the fraction of the year during which interest is earned.
If the investment is made for 3 months, then t = 3 months/12 months = 0.25 years.
If the investment is made for 35 days then t = 35 days/365 days = 7/73 years.
EXAMPLE 2
a) If an investment is made for a period of 145 days, what portion of the year does this represent?
b) If an investment is made for a period of 48 weeks, what portion of the year does this represent?
c) If an investment is made for a period of 10 months, what portion of the year does this represent?
Solution:
a) 145 ÷ 365= 29/73 years
b) 48 ÷ 52 = 12/13 years
c) 10 ÷ 12 = 5/6 years
TRY IT 2
a) If an investment is made for a period of 220 days, what portion of the year does this represent?
b) If an investment is made for a period of 32 weeks, what portion of the year does this represent?
c) If an investment is made for a period of 2 months, what portion of the year does this represent?
Show answer
a) 220 ÷ 365= 44/73 year
b) 32 ÷ 52 = 8/13 year
c) 2 ÷ 12 = 1/6 year
EXAMPLE 3
Determine the interest that will be earned on a deposit of $1350 at 2.8% over:
a) 7 months
b) 25 days
Solution:
a)
|
|
Interest of $22.05 over 7 months
b)
|
|
Interest of $2.59 over 25 days. Note that the answer is rounded to the nearest two decimal places or to the nearest cent.
TRY IT 3
Determine the interest that will be earned on a deposit of $2200 at 4.52% over:
Determine the interest earned after a) 1 month b) 300 days
Show answer
a) $8.29 b) $81.73
EXAMPLE 4
Determine the interest that will be earned on a deposit of $4200 at 4.65% over:
a) ![]() years
years
b) 5 weeks
Solution
a)
|
|
Interest of $292.95 over ![]() years
years
b)
|
|
Interest of $18.78 over 5 weeks. Note that the answer is rounded to the nearest two decimal places or to the nearest cent.
TRY IT 4
Max deposited $1500 in a savings account at an interest rate of 3.28%.
Determine the interest earned after i) 3 months ii) 65 days iii) two years.
Show answer
![]()
![]()
![]()
Maturity Value
The total amount of money due at the end of a loan period is called the maturity value of the loan. It is the amount to be paid on the due date of a loan or the amount to be paid to an investor at the end of the period for which an investment has been made.
Maturity Value
The Maturity Value (MV) of a loan is the sum of the principal P plus the interest I.
MV = P + I
In Example 1, Jo borrowed $2000 at an interest rate of 5%. At the end of one year Jo owed $100 in interest.
The maturity value of the loan is MV = P + I where P = $2000 and I = $100.
MV = $2000 + $100 = $2100
The maturity value of the loan is $2100. At the end of the year Jo will be expected to pay back $2100.
EXAMPLE 5
Linda lends Ed $500. Ed says he will pay her back in 60 days at 9% simple interest. How much interest should Linda receive? How much must Ed pay Linda altogether?
Solution
| Replace P, r and t with their values | ||
| Multiply | ||
| Round to the nearest cent |
MV = P + I = $500 + $7.40 = $507.40
Linda should receive $7.40 in interest. At the end of 60 days Ed will owe Linda $507.40.
TRY IT 5
In order to purchase equipment, a barbershop takes out a short term loan of $3000 at a rate of 4.35%. The loan is due in 80 days.
Determine the interest that will be owed at the end of 80 days and find the maturity value of the loan.
Show answer
Interest owed is $28.60, MV is $3028.60
Variations On Simple Interest
The amount of interest earned on an investment or due on a loan is calculated using I = Prt.
This formula can also be used to determine:
- the amount of principal (P) that needs to be invested in order to earn a certain amount of interest over a certain period of time.
- the interest rate (r) that is needed in order to earn a certain amount of interest over a given time period.
- the amount of time (t) it will take in order to earn a certain amount of interest at a stated interest rate.
These amounts can be determined by solving the simple interest formula for any of r, P or t.
Finding the Principal, Interest Rate, or Time
| where | ||
| To determine the principal use: | I = interest earned | |
| To determine the interest rate use: | r = annual interest rate | |
| To determine the time use: | P = principal | |
| t = time (in years) |
The following memory aid is often called the “Magic Triangle”, because if you cover the variable you are trying to find, the formula will magically appear!
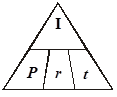
Determining the Principal
EXAMPLE 6
A six month investment will earn 5.25%. How much would you need to invest if you want to earn $100 in interest?
Solution
The principal is unknown. Cover P in the Magic Triangle.
P = ? or 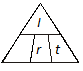 appears. Use the formula:
appears. Use the formula: ![]()
![]()
![]()
| Replace I, r and t with their respective values | ||
| Multiply 0.0525 by 0.5 | ||
| Divide 100 by 0.02625 and round answer to nearest cent |
You would need to invest $3809.52
TRY IT 6
A student borrowed money from his best friend at the very low interest rate of 1.5% for a period of 9 months. At the end of 9 months the friend had earned $22.50 in interest. Determine the original amount of the loan.
Show answer
![]()
Determining the Interest Rate
EXAMPLE 7
Mariko had $240 in the bank for the month of April. At the end of the month she had earned $0.90 in interest. What interest rate was the bank paying?
Solution
The interest rate is unknown. Cover r in the Magic Triangle.
r = ? or 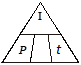 appears. Use the formula:
appears. Use the formula: ![]()
t = 1 month = |
|
Since r = 0.045, the interest rate as a percentage is 4.5%
TRY IT 7
Kris deposited $800 in an account. At the end of 6 months he had earned $10.40. Determine the interest rate.
Show answer
![]()
Determining the Time
EXAMPLE 8
Carol invested $500 at an interest rate of 6%. How long will it take her to earn $250 in interest?
Solution
The time is unknown. Cover t in the Magic Triangle.
t = ? or 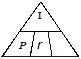 appears. Use
appears. Use ![]()
r = 6% = 0.06 |
|
It will take 8.33 years.
TRY IT 8
An account earns 4% interest. How long will it take for a deposit of $4000 to earn $240 in interest?
Show answer
![]()
When calculating time “t” using the simple interest formula, the answer will be in terms of years. Sometimes it is more reasonable to express the answer in terms of days or months.
Time Conversions
When converting time (in years) to months or days:
To express the time in months (m):
Multiply the time “t” in years x 12 months/year.
If time t = 0.25 years then the number of months m = 0.25 years x 12 months/year = 3 months
To express the time in days (d):
Multiply the time “t” in years x 365 days/year.
If time t = 0.25 years then the number of days d = 0.25 years x 365 days/year = 91.25 days
EXAMPLE 9
Troy invested $4000 in an account offering 3.8%. How long will it take him, in days, to earn $30 in interest?
Solution
![]() =
= ![]()
Time in days = 0.1974 years x 365 days/year = 72 days
It will take 72 days to earn $30 in interest
TRY IT 9
Tam invested $1875 in an account offering 4%. How long will it take her, in months, to earn $62.50 in interest?
Show answer
![]() years so 0.833… years
years so 0.833… years ![]() 12 = 10 months
12 = 10 months
Key Concepts
- to calculate the simple interest earned on an investment or charged on a loan we use the formula I = Prt where:
I = interest earned r = annual interest rate ( stated as a decimal)
P = principal amount t = time (in years)
- to determine the principal amount (P) for simple interest applications:
- to determine the time in years (t) for simple interest applications:
- to determine the interest rate (r) for simple interest applications:
- The Maturity Value (MV) of a loan is the sum of the principal P plus the interest I:
MV = P + I
Glossary
maturity value
is the amount to be paid on the due date of a loan or the amount to be paid to an investor at the end of the period for which an investment has been made.
principal
is the amount of money that has been invested or borrowed.
simple interest
is interest that is calculated only once during the entire time period of the loan or deposit. Simple interest is calculated solely on the principal investment or loan.
Attribution
Some of the content for this chapter is from “Unit 1: Simple interest” and “Unit 2: Variations on simple interest” in Financial Mathematics by Paul Grinder, Velma McKay, Kim Moshenko, and Ada Sarsiat, which is under a CC BY 4.0 Licence.. Adapted by Kim Moshenko. See the Copyright page for more information.
9.2 Compound Interest

Learning Objectives
By the end of this section it is expected that you will be able to:
- Determine the compound amount (future value) of an investment or loan
- Determine the interest component of an investment or loan that involves compound interest
- Determine the present value of a compound amount
Compound Interest
We have seen that with simple interest an investment will earn interest on the original amount. For an investment of $100 earning 10% simple interest, the interest earned after one year will be $10 since 10% of $100 = $10. An investment will grow more quickly if the interest is calculated more often than once a year. Interest will not only be calculated on the principal amount but also on the previously earned interest. This process is referred to compounding.
Figure 1 illustrates the process of compounding or earning interest on interest. Consider an investment of $100 that earns 10%/year with interest being compounded semiannually. With semiannual compounding the interest on the investment will be calculated twice during the year.
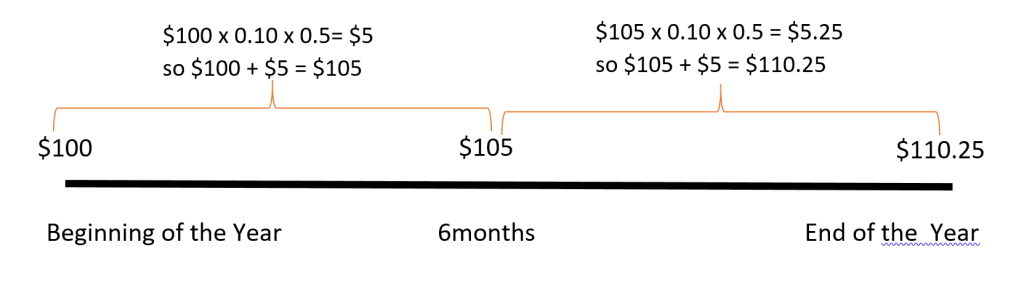
Using the simple interest formula I = Prt, at the end of six months (half a year) interest will be calculated as follows:
I = $100 x 10% x 1/2 year = $5.
Adding this $5 to the principal of $100 you will have $105 at the end of the first six months. At the end of the year interest will be calculated again on the $105:
I = $105 x 10% x 1/2 year = $5.25.
Adding this $5.25 to $105 you will have $110.25 at the end of the year. In this case you would be earning interest not only on the original principal of $100, but also on the previously earned interest of $5. When interest is earned on interest, we say the interest is compounded. The total amount of principal and accumulated interest at the end of a loan or investment is called the compound amount.
Consider a $100 investment that earns 10%/year compounded annually. The table in Figure 2 shows how the value of the $100 investment will grow over a 6-year period.
| Year | Amount at the beginning of the year | Earned Interest | Year End Total |
|---|---|---|---|
| 1 | $100 | $10 | $110 |
| 2 | $110 | $11 | $121 |
| 3 | $121 | $12.10 | $133.10 |
| 4 | $133.10 | $13.31 | $146.41 |
| 5 | $146.41 | $14.64 | $161.05 |
| 6 | $161.05 | $16.11 | $177.16 |
Fig. 2
At the beginning of Year 1, $100 is invested, so the interest earned in the first year will be:
I = Prt = $100 × 0.10 × 1 = $10. This is added to the original $100 to result in $110 at the end of Year 1.
At the beginning of Year 2 the process will repeat but the principal P is now $110.
I = Prt = $110 × 0.10 ×1 = $11 in interest so at the end of Year 2 there will be:
$110 + $11 = $121 in the account.
Notice that the compound amount at the end of the six year period is $177.16. The investment has earned an accumulated $77.16 in interest. If the investment had earned simple interest as opposed to compound interest it would have only earned:
I = Prt = 100 × 0.10 × 6 = $60 in interest.
The above method of calculating the compound amount is very time consuming. Fortunately, there is a mathematical formula that we can use when working with compound interest.
Compound Interest Formula
The compound interest formula is:
| where, | A = total compound amount(includes principal and interest) | |
| P = principal | ||
| r = annual interest rate | ||
| n = number of times in one year that interest is calculated | ||
| t = time (in years) |
Since A includes both the principal and interest, to find the interest amount I calculate:
![]()
EXAMPLE 1
Find the compound amount and the interest earned on $100 compounded annually at 10% for 6 years.
Solution
| P = $100
r = 10% = 0.1 n = 1 (since the interest is calculated once a year) t = 6 years |
|
Replace the variables with their values |
| Raise |
||
The interest earned is ![]() $77.16
$77.16
The compound amount is $177.16
TRY IT 1
Kyle won $10,000 in a lottery and deposited the full amount in a 3 year investment at 3.8% compounded annually. Find the compound amount and the interest earned over the three years.
Show answer
Compound Amount = $11,183.87; Interest = $1183.87
Interest can be compounded using a variety of compounding periods. The compounding period is the span of time between when interest is calculated and when it will be calculated again. If there is one month between every interest calculation then the compounding period is monthly. With monthly compounding there will be 12 compounding period in one year since there are twelve months in a year . The variable n in the compound interest formula reflects the number of times in one year that interest is calculated.
Compounding Periods
If interest is compounded:
annually (once per year) ⇒ n = 1
semi-annually (twice a year) ⇒ n = 2
quarterly (four times per year) ⇒ n = 4
monthly (twelve times per year) ⇒ n = 12
weekly (fifty-two times per year) ⇒ n = 52
daily (three hundred sixty-five times per year) ⇒ n = 365
EXAMPLE 2
Find the compound amount and the interest earned on $500 compounded semiannually at 6% for 3 years.
Solution
The compound amount is $597.03 and the interest earned is $597.03 – $500 = $97.03
TRY IT 2
Kam won $10,000 in a lottery and deposited the full amount in a 3 year investment at 3.8% compounded monthly. Find the compound amount and the interest earned over the three years.
Show answer
Compound Amount = $11,205.50; Interest = $1205.50
The greater the number of compounding periods in a year, the greater the total interest earned will be.
EXAMPLE 3
Find the compound amount and the interest earned on $500 compounded daily at 6% for 3 years.
Solution
The compound amount is $598.60 and the interest earned is $598.60 – $500 = $98.60
TRY IT 3
Kam won $10,000 in a lottery and deposited the full amount in a 3 year investment at 3.8% compounded daily. Find the compound amount and the interest earned over the three years.
Show answer
Compound Amount = $11,207.45; Interest = $1207.45
Loan recipients must repay the principal amount borrowerd plus any interest charged. They will pay a greater price (in terms of total interest) when interest is compounded.
EXAMPLE 4
Pat borrows $3200 an interest rate of 6.5% compounded semiannually. The original loan amount plus interest must be paid back in 3 years. Calculate the total amount that must be paid back in three years and determine the interest amount.
Solution
The compound amount is $3876.95 and the interest owing is $3876.95 – $3200 = $676.95
TRY IT 4
Determine the compound interest on a 2 year loan of $5000 at an interest rate of 4.8% compounded quarterly.
Show answer
Compound Amount = $5500.65; Interest = $500.65
EXAMPLE 5
Pat borrows $3200 an interest rate of 6.5% compounded monthly. The original loan amount plus interest must be paid back in 3 years. Calculate the total amount that must be paid back in three years and determine the interest amount.
Solution
The compound amount is $3886.95 and the interest owing is $3886.95 – $3200 = $686.95
TRY IT 5
Determine the compound interest on a 2 year loan of $5000 at an interest rate of 4.8% compounded daily.
Show answer
Compound Amount = $5503.76; Interest = $503.76
Variation on Compound Interest – Present Value
We might want to know how much money we should invest now in order to make a purchase in the future. Say for example that you want to know how much principal you needed to invest now in order to have $2000 in two years. The amount you need to invest now is called the present value of $2000. It is the amount of money that if invested now will accumulate to $2000 in two years. Assuming that your investment earns interest, the amount required now will be less than the future amount. Assuming annual compounding at an interest rate of 5% you will need to invest $1814.06 now to have $2000 in two years. Refer to Figure 3 below.
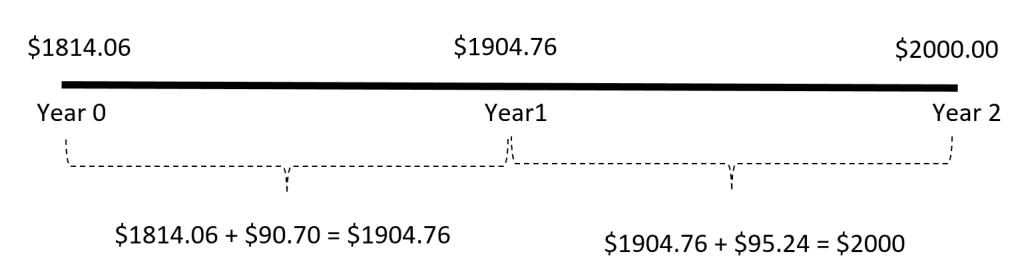
In Figure 3 we can see that at the beginning of the year $1814.06 is invested.
At the end of the first year the interest earned on $1814.06 is 5% × 1814.06 = $90.70.
At the end of the first year there will be $1904.76 in the account. In the second year the interest earned on $1904.76 is $1904.76 × 0.05 = $95.24.
At th eend of the second year there will be $2000.00 in the account. The $2000 that is needed in two years is said to have a present value of $1814.06.
The present value can be calculated by solving the compound interest formula for P.
Formula for Present Value
The present value formula is:
![]()
| where | P = present value |
| A = desired future amount | |
| r = interest rate (as a decimal fraction) | |
| n = number of times interest is calculated in one year | |
| t = times (in years) |
EXAMPLE 6
A house painting company is planning to expand its operations in three years time. It will require $24,000 in order to expand. How much must it invest now, at 4.6% interest compounded annually?
Solution
| P = ?
A = $24000 r = 4.6% = 0.046 n = 1 |
||
| t = 3 years | Replace the variables with their values | |
| Add |
||
| Raise |
||
The present value is $20,970.86 so the company must invest that amount now to have $24,000 in three years.
TRY IT 6
Mae is planning on buying a vehicle when she turns 18 in five years. How much money must she invest now in an account earning 7% interest, compounded annually, in order to afford a used vehicle at a cost of $5000?
Show answer
An investment of $3564.93 is required
EXAMPLE 7
Pat and her friends are planning a reunion in five years. She estimates that the cost of the trip plus expenses will be approximately $2000. How much should she invest right now in order to have $2000 five years from now, if she knows her money will earn 6% compounded quarterly?
Solution
| P = ?
A = $2000 r = 6% = 0.06 n = 4 |
||
| t = 5 years | Replace the variables with their values | |
| Multiply |
||
| Divide |
||
| Add |
||
| Raise |
||
The present value is $1484.94
In other words, if Pat invested $1484.94 now at 6% compounded quarterly, then in 5 years the compound amount would be $2000.
TRY IT 7
You are planning on attending college in four years and your parents plan to help out with $10,000 in assistance. How much money must they invest now in an account earning 5.6% compounded monthly if they plan to have $10000 in the account in four years?
Show answer
$7997.31
Key Concepts
- to determine the compound amount (A) of an investment or loan:
- to determine the interest component (I) of a principal or original amount (P) that has grown to a compound amount (A):
- Interest = Compound Amount – Principal Amount I = A – P
- to determine the present value P of a compound amount the formula is:
- Compounding Periods
- annually (once per year) ⇒ n = 1
- semi-annually (twice a year) ⇒ n = 2
- quarterly (four times per year) ⇒ n = 4
- monthly (twelve times per year) ⇒ n = 12
- weekly (fifty-two times per year) ⇒ n = 52
- daily (three hundred sixty-five times per year) ⇒ n = 365
Glossary
compound amount
is the total amount of principal and accumulated interest at the end of a loan or investment period.
compound interest
is when the interest on a loan or deposit is calculated based on both the initial principal and any accumulated interest from previous periods.
compounding period
is the span of time between when interest is calculated and when it will be calculated again.
present value
is the current value of a sum of money that has been invested and has grown to a larger compound amount.
Attribution
Some of the content for this chapter is from “Unit 3: Compound interest” and “Unit 4: Variations on compound interest – present value” in Financial Mathematics by Paul Grinder, Velma McKay, Kim Moshenko, and Ada Sarsiat, which is under a CC BY 4.0 Licence.. Adapted by Kim Moshenko. See the Copyright page for more information.
9.3 Interest Rates

Learning Objectives
By the end of this section it is expected that you will be able to:
- State the difference between nominal and effective interest rates
- Determine the effective annual interest rate
- Determine the best option when comparing nominal interest rates under different situations
Nominal and Effective Rates of Interest
As consumers and investors we are inundated with all kinds of offers for both investments and financing. When we require a loan we seek the lowest possible interest rate but when we invest we want the highest rate of return. As we search for the best offer it is important to recognize that the advertised interest rate is not necessarily the true interest rate.
An advertised rate of 10% with annual compounding works out to be equivalent to a rate of 10% annually. We refer to this stated rate of 10% as the nominal interest rate. An advertised rate of 10% with daily compounding works out to be equivalent to a rate of 10.52% since interest is calculated on the interest 365 times in one year. We refer to the 10.52% as the effective interest rate.
The stated interest rate is referred to as the nominal interest rate, as it describes the named or numerical value. It is the rate that is usually stated in advertisements. The actual interest rate, or effective interest rate, reflects the real rate of return as it takes the compounding periods into account.
With simple interest calculations (where there is no compounding), the stated annual interest rate indicates the true rate of return. If $1000 is borrowed at 6% for one year, then the interest owined will be I = Prt = $1000 × 0.06/yr × 1yr = $60.
With compound interest calculations, the stated annual interest rate does not indicate the true interest cost. If $1000 is invested at 6% for one year compounded semiannually, then the interest owed will be $60.90 rather than $60.
One way to determine the effective interest rate is to divide the total compound interest for the first year by the principal amount. If in the first year $60.90 is the interest charged on a principal of $1000 then the effective interest rate is $60.90/$1000 = 0.0609 = 6.09%. Although the nominal interest rate is 6%, the effective rate is 6.09%.
It is also possible to use a formula to calculate the effective interest rate.
Effective Interest Rate Formula
The effective interest rate formula is:
| where | f = effective interest rate | |
| r = nominal interest rate (annual interest rate) | ||
| n = number of times in one year that interest is calculated |
EXAMPLE 1
Use the formula to determine the effective interest rate for 6% compounded annually.
Solution
| f = ?
r = 6% = 0.06 n = 1 |
||
| Replace the variables with their values | ||
| Add |
||
The effective interest rate is 6%. Note that the nominal and effective rate are the same since the number of compounding period is one (n = 1).
TRY IT 1
What is the effective rate of 4% compounded yearly?
Show answer
4%
EXAMPLE 2
Use the formula to determine the effective interest rate for 6% compounded monthly.
Solution
| f = ?
r = 6% = 0.06 n = 12 |
||
| Replace the variables with their values | ||
| Divide |
||
| Add |
||
| Raise |
||
The effective interest rate is 6.17%
TRY IT 2
What is the effective rate of 4% compounded monthly?
Show answer
4.07%
EXAMPLE 3
What is the effective rate for a nominal rate of 9.8% compounded weekly?
Solution
| f = ?
r = 9.8% = 0.098 n = 52 |
||
| Replace the variables with their values | ||
| Divide |
||
| Add |
||
| Raise |
||
|
|
The effective interest rate is 10.29%
TRY IT 3
Determine the effective rate of interest on a loan that is advertised at a rate of 7.8% compounded daily.
Show answer
8.11%
It is important to consider the effective interest rate, rather than the nominal rate, when deciding on investments or loans.
Consider Bank A which offers a savings plan at 6.25% compounded monthly and Bank B which offers 6.5% compounded semi-annually. Which of the two banks offers the better rate of return? Although both banks offer the same nominal interest rate, their effective rates differ. The effective rate will reflect the actual rate of return in one year. Example 4 will illustrate this.
EXAMPLE 4
Bank A offers 6.25% compounded monthly while Bank B offers 6.5% compounded semi-annually. Which bank offers the better effective rate of return?
Solution
For Bank A:
| f = ?
r = 6.25% = 0.0625 n = 12 |
|
For Bank B:
| f = ?
r = 6.5% = 0.065 n = 2 |
|
Note that Bank A’s effective rate, 6.43%, is less than both Bank B’s nominal rate of 6.5% and Bank B’s effective rate of 6.61%. Bank B offers the better effective rate of return.
TRY IT 4
Sam plans to invest a lottery win of $15,000. He is considering two different options. Option A offers 3.56% compounded weekly and Option B offers 3.48% componded monthly. Which option offers a better rate of return?
Show answer
Option A 3.62%; Option B 3.54%; Option A offers a better rate of return.
EXAMPLE 5
Consider two options for a 2 year loan. Bank A will charge 7.2% compounded monthly while Bank B will charge 7.4% compounded semi-annually. Which bank offers the less expensive loan (charges the lower effective rate)?
Solution
For Bank A:
| f = ?
r = 7.2% = 0.072 n = 12 |
|
For Bank B:
| f = ?
r = 7.4% = 0.074 n = 2 |
|
Bank A’s effective rate, 7.44%, is less than Bank B’s effective rate of 7.54. By a slight margin, Bank A offers the less expensive loan.
TRY IT 5
Sam needs to borrow $5500. He is offered two different loans. One loan is at a bank for 6.8% compounded quarterly and the other is at a credit union for 6.9% compounded semiannually.
Which is the better option for Sam?
Show answer
Bank 6.98%; Credit Union 7.02%; the Bank is a slightly better option for a loan.
Key Concepts
- to determine the effective annual interest rate (f):
- when investing money you want the higher effective interest rate; when borrowing money you want the lower effective interest rate.
Glossary
effective interest rate
takes the compounding periods into effect so it is a better reflection of the actual interest charges.
nominal interest rate
is normally the stated rate. It does not take the compounding periods into effect.
Attribution
Some of the content for this chapter is from “Unit 5: Nominal and effective rates of interest” in Financial Mathematics by Paul Grinder, Velma McKay, Kim Moshenko, and Ada Sarsiat, which is under a CC BY 4.0 Licence.. Adapted by Kim Moshenko. See the Copyright page for more information.
9.4 Loans and Mortgages

Learning Objectives
By the end of this section it is expected that you will be able to:
- Determine the periodic payments on an installment loan
- Determine the amount financed and the finance charge on an installment loan
- Determine the payments and finance charge on a mortgage
Installment Loans
A loan is something that is borrowed. In the case where this is a sum of money the amount that will be paid by the borrower will include the original amount plus interest.
Some loans require full payment on the maturity date of the loan. The maturity date is when all principal and/or interest must be repaid to the the lender. Consider a one year loan of $1000 at a simple interest rate of 5%. At the end of one year (the maturity date) the borrower will pay back the original $1000 plus the interest of $50 for a total of $1050.
For major purchases such as vehicles or furniture there is a different type of loan, called the installment loan. The average consumer cannot afford to pay $25000 or more for a new vehicle and they may not want to wait three or four years until they have saved enough money to do so. The qualifying consumer has the option of paying for the item with an installment loan.
Installment loans do not require full repayment of the loan on a specific date. With an installment loan the borrower is required to make regular (installment) payments until the loan is paid off. Each installment payment will include an interest charge. An installment loan can vary in length from a few years to perhaps twenty years or more (in the case of real estate).
Consider an installment loan for a $4000 television. The purchaser takes out a $4000 loan with a four-year term at an interest rate of 4.5%. The monthly installment payments will be $91.21. Although the television has a purchase price of $4000, the total cost to the purchaser will be more than $4000. The total of the installment payments will be:
Total Installment Payments = Number of Installment Payments x Payment Amount =
4 years x 12 payments/year x $91.21/mth = $4378.08
The $4000 television ends up costing $4378.08 because the consumer is charged interest. Each payment includes an interest component that adds to the overall cost of the item. The total of the interest charges is referred to as the finance charge on the loan.
Finance Charge
The finance charge is the sum of the interest charges on a loan. These interest charges are embedded in the installment payments. To calculate the finance charge:
Finance Charge = Total Installment Payments – Loan Amount
= (Number of Installment Payments x Payment Amount) – Loan Amount
For the $4000 television the finance charge will be calculated as follows:
Finance charge = Total Installment Payments – Loan Amount =
(4 years x 12 payments/year x $91.21/payment) – $4000 = $4378.08 – $4000 = $378.08
Over the 4-year term of the loan the purchaser will have paid the $4000 loan amount plus an additional $378.08 in interest (the finance charge).
Sometimes the borrower will make an initial payment at the time of purchase. This is called a down payment. When a down payment is made the remaining amount is the amount financed or the loan amount.
Amount Financed
The amount financed or loan amount is the purchase price of the item less any down payment:
Amount Financed = Purchase Price – Down Payment
Consider the $4000 television. Assume the purchaser makes a down payment of $1500.
The amount financed is: Purchase Price – Down Payment = $4000 – $1500 = $2500.
In this case the purchaser borrows $2500 rather than $4000. The amount financed is therefore $2500. Assuming the same 4-year term and an interest rate of 4.5%, the installment payments on the $2500 will be reduced to $57.01 per month. In this case the finance charge will be calculated as follows:
Finance charge = Total Installment Payments – Loan Amount =
(4 years x 12 payments/year x $57.01/payment) – $2500 = $2736.48 – $2500 = $236.48
With the down payment of $2500 the total finance charges will be reduced to $236.48 from $378.08.
The total cost of the television to the purchaser will be:
Purchase Price + Finance Charge
= $4000 + $236.48 = $4236.48
Alternatively we can calculate:
Total Installment Payment + Down Payment
= $2736.48 + $1500 = $4236.48
As one can see, the finance charges are a hidden but added cost. This cost will become more pronounced with more expensive purchases such as with real estate.
Installment Loan Terminology
Total Installment Payments = Number of payments x Payment Amount
Finance Charge = Total Installment Payments – Loan Amount
Amount Financed or Loan Amount = Purchase Price of Item – Down payment
EXAMPLE 1
Paul purchased a home entertainment system at a total cost of $6000. He obtained a 3 year loan at an interest rate of 7.5%. His monthly payments will be $186.64 over three years.
a) State the amount financed.
b) Determine the total installment payments.
c) Determine the finance charge.
Solution
a) Since there was no down payment the amount financed (or loan amount) will be $6000.
b) The total installment payments will be:
Number of payments x Payment Amount
= 3 years x 12 payments/year x $186.64
= $6719.04
c) Finance Charge = Total installment payments – Loan Amount
= $6719.04 – $6000
= $719.04
TRY IT 1
Cassie purchased a new washer and dryer at a total cost of $3800. She obtained a 4 year loan at an interest rate of 6.2%. Her monthly payments will be $89.59 over four years.
a) State the amount financed.
b) Determine the the total installment payments.
c) Determine the finance charge.
Show answer
a) $3800.00 b) $4300.32 c) $500.32
EXAMPLE 2
Mike purchased a home entertainment system at a total cost of $6000. He made a down payment of $1800 and to pay the balance he obtained a 3 year loan at an interest rate of 7.5%. His monthly payments will be $130.65 over three years.
a) State the amount financed.
b) Determine the total installment payments.
c) Determine the finance charge.
d) Determine the total amount that Mike paid for the home entertainment system
Solution
a) Amount Financed = Cost of Item – Down Payment
= $6000 – $1800 = $4200
b) The total installment payments will be:
Number of payments x Payment Amount = 3 years x 12 payments/year x $130.65
= $4703.40
c) Finance Charge = Total installment payments – Loan Amount
= $4703.40 – $4200
= $503.40
d) Total paid = Purchase Price + Finance Charge = $6000 + $503.40 = $6503.40
TRY IT 2
Carl purchased a new washer and dryer at a total cost of $3800. He made a down payment of $1500 and obtained a 2 year loan for the remaining amount at an interest rate of 6.2%. His monthly payments will be $102.14 over two years.
a) State the amount financed.
b) Determine the total installment payments.
c) Determine the finance charge.
d) Determine the total amount that Carl paid for the washer and dryer.
Show answer
a) $2300.00 b) $2451.36
c) $151.36 d) $3951.36
Loan Payments
Periodic Payment on a Loan
The periodic payment on a loan formula is:
![]()
| P = periodic payment amount |
| A = amount of loan |
| r = annual interest rate (in decimal form) |
| n = number of payments made in one year |
| t = time (in years) |
EXAMPLE 3
Refer back to the purchase of a television for $4000. The purchaser agrees to a 4 year term at an interest rate of 4.5%. a) Use the formula to determine the monthly installment payment b) Determine the total installment payments
Solution
a)
![]()
where P = payment (unknown), A = $4000, r = 4.5%, n = 12, t = 4 years
![]()
The monthly payment is confirmed to be $91.21.
b) Total installment payments = monthly payment amount x no. of payments
$91.21 x 48= $4378.08
TRY IT 3
A dining room table set is purchased for $5600. The purchase is financed with a 3 year loan at an interest rate of 12.5%. a) Use the formula to determine the monthly installment payment b) Determine the total installment payments.
Show answer
Monthly payment is $187.34; Total Installment payments ![]()
EXAMPLE 4
Paul purchased a home entertainment system at a total cost of $6000. He obtained a 3 year loan at an interest rate of 7.5%. Use the formula to determine his monthly payments. Confirm that this matches the amount in Example 1.
Solution
|
|
P = payment (unknown) | |
| where | A = $6000 r = 7.5% | |
| n = 12 t = 3 years |
![]()
The monthly payment is confirmed to be $186.64
TRY IT 4
Cassie purchased a new washer and dryer at a total cost of $3800. She obtained a 4 year loan at an interest rate of 6.2%. Use the formula to determine her monthly payments. Confirm that this matches the amount in Try It 1.
Show answer
Monthly payment of $89.59 is confirmed
EXAMPLE 5
Determine a) the annual payments b)the total installment payments and c) the finance charge on a 5 year loan of $5000 where payments are made annually and the interest rate is 6%.
Solution
a)
![]()
P = payment
A = $5000 r = 6%
n = 1 t = 5 years
![]()
The annual payment will be $1186.98.
b) Total installment payments = $1186.98 x 5 = $5934.90
c) Finance charge = $5934.90 – $5000 = $934.90
TRY IT 5
Determine a) the annual payments b) the total installment payments and c) the finance charge on a 5 year loan of $5000 where payments are made monthly and the interest rate is 6%.
Show answer
a) Annual payment is $96.67
b) Total Installment payments = $5800.20
c) Finance charge $800.20
Recall that interest is calculated only on the loan amount and not on any downpayment. When determining the periodic payment on an installment loan be sure to exclude the downpayment when calculating the periodic payment.
EXAMPLE 6
Mike purchased a home entertainment system at a total cost of $6000. He made a down payment of $1800 and to pay the balance he obtained a 3 year loan at an interest rate of 7.5%. Use the formula to determine his monthly payments. Confirm that this matches the amount provided in Example 2.
Solution
|
|
P = payment (unknown) | |
| where | A = $4200 r = 7.5% | |
| n = 12 t = 3 years |
![]()
The monthly payment is confirmed to be $130.65
TRY IT 6
Carl purchased a new washer and dryer at a total cost of $3800. He made a down payment of $1500 and obtained a 2 year loan for the remaining amount at an interest rate of 6.2%. Use the formula to determine his monthly payments. Confirm that this matches the amount provided in Try It 2.
Show answer
Monthly payment of $102.14 is confirmed
EXAMPLE 7
Pat has decided to purchase a used vehicle that costs $12,500. He considers two options. For each option, determine a) the monthly payment b) total installment payments c) the finance charge for each option. What is the difference in the finance charge with the down payment?
Option 1) Paying the full amount with a 4 year loan, monthly payments, and an interest rate of 6.8%.
Option 2) He will cancel a planned trip and and instead make a $3500 down payment on the purchase. He will pay the remaining amount with a 4 year loan, monthly payments, and an interest rate of 6.8%.
Solution
Option 1)
a) P = unknown A = $12,500
r = 0.068 n = 12 t = 4
b) Total Installment payments ![]()
c) Finance charge = Total Installment Payments – Loan Amount = $14312.16 – $12,500 = $1812.16
Option 2)
a) P = unknown A = $12,500 – $3500 =$9000
r = 0.068 n = 12 t = 4
b) Total Installment payments ![]()
c) Finance charge = Total Installment Payments – Loan Amount = $10,304.64 – $9000 = $1304.64
With a down payment there will be a savings of $507.52 on the finance charges.
TRY IT 7
Mick has decided to purchase a home entertainment system at a cost of $9200. He considers two options. For each option determine a) the monthly payment b) total installment payments c) the finance charge for each option. What is the difference in the finance charge with the down payment?
1) Paying the full amount with a 3 year loan that offers an interest rate of 8.4%.
2) Forgoing the purchase of a new electric bike and instead makinga $2000 down payment on the bike purchase. He will pay the remaining amount with a 3 year loan at an interest rate of 8.4%.
Show answer
With no down payment: a) $290 b) $10440 c) $1239.83
With a down payment a) $226.95 b) $10170.20 c) $970.30; With the down payment the finance charge is $269.53 less
Amortization
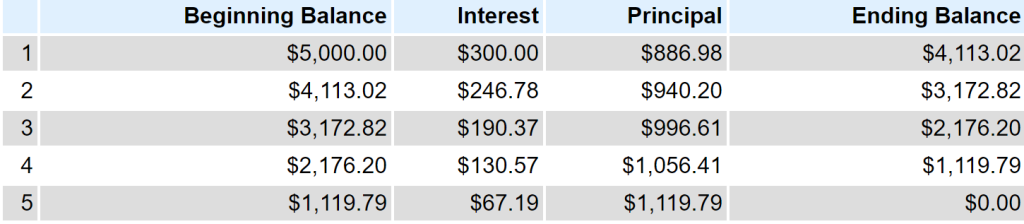
The cycle repeats for five years until the loan is paid off. If we add the interest charges in the table they will total to $934.91. This is the same as the finance charge (ignoring the 1¢ difference due to rounding) that was calculated in Example 5.
Mortgages
A long term loan that is used for the purchase of a house is called a mortgage. It is called a mortgage because the lending agency requires that the house be used as collateral for the loan. This means that if the mortgage holder is unable to make the payments the lender can take possession of the house.
Mortgages generally tend to be for longer time periods than an installment loan and the terms of the mortgage will often change over the course of the mortgage. Take for example the purchase of a house with a twenty year mortgage. The purchaser might sign a mortgage agreement for a five year term. The mortgage agreement will include the interest rate, the frequency of payments and additional rules which may allow the mortgage holder to make lump sum payments or change the payment amount. At the end of the five year term a new agreement will be required and the conditions of the mortgage usually change.
Although it is possible to do the calculations manually, that is beyond the scope of this book. We will use technology to calculate the periodic payments and interest charges and to generate an amortization schedule.
Example 8 will illustrate that amortizing a mortgage is similar to amortizing other loans except that the mortgage amortization generally involves many more payment periods.
EXAMPLE 8
A $400,000 home is purchased with a 20% down payment on a 20-year mortgage at a fixed interest rate of 3.4%.
a) Determine the down payment.
b) Use an online mortgage calculator to determine the monthly payment and the total interest paid.
c) Generate an annual amortization schedule.
d) Determine the total payments for one year
e) Use the table to determine how much of the first year’s payments will go towards interest and how much will go towards the principal.
f) Use the table to determine how much of the final year’s payments will go towards interest and how much will go towards the principal.
Solution:
a) The down payment will be 20% x $400,000 = $80,000.
b) The monthly payment will be $1839.47 and the total interest will be $121, 472.75.
c)
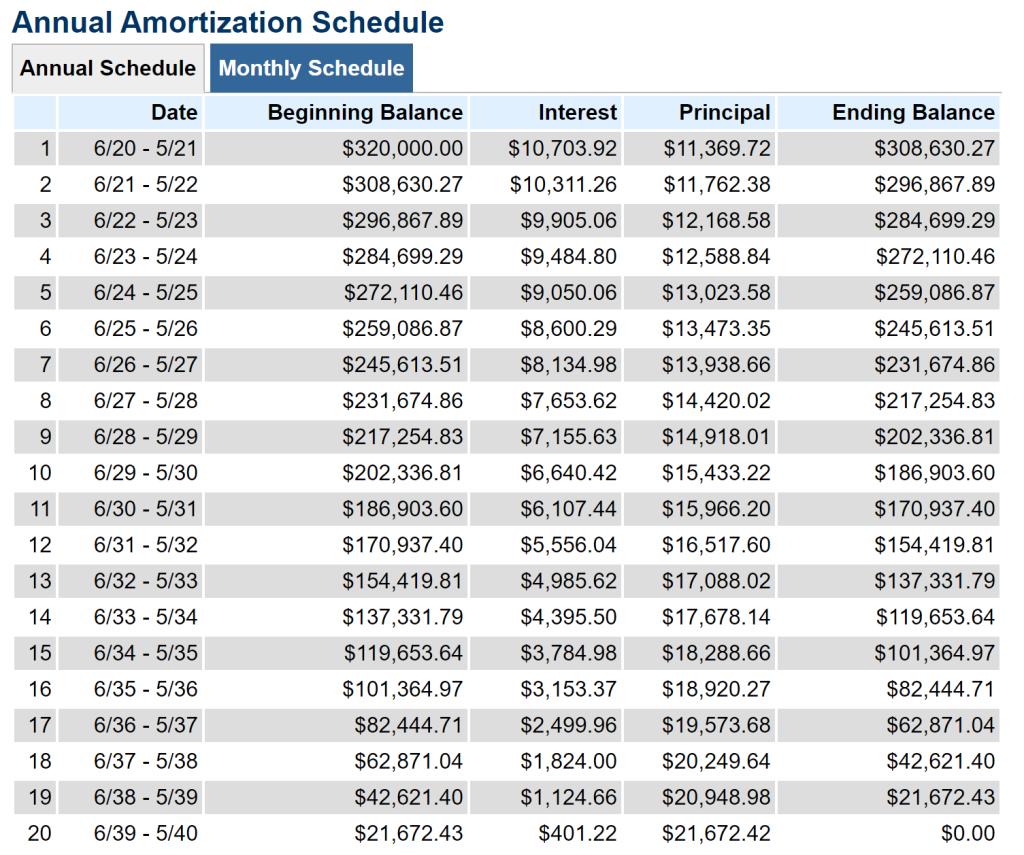
d) In one year the total payments will be 12 x $1839.47 = $22,073.64.
e) Of the first year’s payments, almost half, $10,703.92, will go towards interest. $11,369.72 will go towards paying down the principal.
f) Of the final year’s payments, $401.22 will go towards interest. $21, 672.42 will go towards the principal.
TRY IT 8
A 20-year mortgage is obtained to purchase a $550,000 home with a 15% down payment at a fixed interest rate of 4.6%.
a) Determine the down payment.
b) Use an online mortgage calculator to determine the monthly payment and the total interest paid.
c) Generate an annual amortization schedule.
d) Determine the total payments for one year
e) Use the table to determine how much of the first year’s payments will go towards interest and how much will go towards the principal.
f) Use the table to determine how much of the final year’s payments will go towards interest and how much will go towards the principal.
Show answer
a) The down payment will be $82,500
b) the monthly payment will be $2982.93 and the total interest will be $248,403.36
d) In the first year the total payments will be $35,795.16.
e) In the first year $21,199.84, will go to interest. $14,595.32 will go towards paying down the principal.
f) In the final year $876.17 will go to interest. $34,918.99 will go towards paying down the principal.
EXAMPLE 9
A young couple have received an inheritance and they now have enough money for a down payment on their first home. They plan to take out a 25 year mortgage at an interest rate of 3.8%. They are considering a new house for $750,000 or a smaller older home for $380,000. If they purchase the larger house they plan to make a 20% down payment. With the less expensive smaller house they can afford a 35% down payment.
a) Use an online mortgage calculator to determine the down payment, the monthly payment and the total interest paid for each of the two houses.
b) For each of the houses, what is the principal balance owing after 5 years?
Solution
a) $750,000 house: $150,000 down payment; $3101.14 monthly payment; Total interest $330,341.81
$380,000 house: $133,000 down payment; $1276.64 monthly payment; Total interest $135,990.71
b) $750,000 house: After 5 years the balance owing is $520,767.80
$380, 000 house: After 5 years the balance owing is $214,382.74
TRY IT 9
A couple has won $50,000 in the lottery and they decide to put this towards the purchase of a vacation cottage or a house. They plan to make a 10% down payment and are considering a 25 year mortgage at a rate of 2.9%. They are deciding between the purchase of a cottage for $500,000 or a house for $880,000.
a) Use an online mortgage calculator to determine the down payment, the monthly payment and the total interest paid for the cottage and for the house.
b) For each of the cottage and the house, what is the principal balance owing after 5 years?
Show answer
a) Cottage: The down payment will be $50,000, the monthly payment will be $2110.62 and the total interest will be $183,185.76
House: The down payment will be $88,000, the monthly payment will be $3714.69 and the total interest will be $322,406.93
b) Cottage: After 5 years the balance owing is $384,024.74
House: After 5 years the balance owing is $675,883.55
Key Concepts
- For an Installment Loan:
- to determine the total installment payments:
Number of Payments x Payment Amount
- to determine the finance (interest) charge:
Total Installment Payments – Loan Amount
- to determine the amount financed:
- to determine the total installment payments:
Purchase Price – Down Payment
-
- to determine the total amount paid for the item:
Purchase Price + Finance Charge
or
Total Installment Payments + Down Payment
-
- to determine the periodic payment P:
![]()
Glossary
amortization
is the process of spreading out a loan into a series of fixed payments.
amount financed
is the purchase price of the item less any down payment.
finance charge
is the total of the interest charges on a loan.
installment loan
is a type of loan that is repaid over time with a set number of scheduled payments (installments). The term of loan may be vary and could be few months or many years.
maturity date
is when all principal and/or interest must be repaid to the lender.

