13 Lesson 3
Izabela Mazur and Kim Moshenko
Percentages
Your class just wrote its first math quiz. You got 13 out of 19 questions correct, or . In speaking with your friends Sandhu and Illija, who are in other classes, you find out that they also wrote math quizzes; however, theirs were different. Sandhu scored 16 out of 23, or
, while Illija got 11 out of 16, or
. Who achieved the highest grade? Who had the lowest? The answers are not readily apparent, because fractions are difficult to compare.
Now express your grades in percentages rather than fractions. You scored 68%, Sandhu scored 70%, and Illija scored 69%. Notice you can easily answer the questions now. The advantage of percentages is that they facilitate comparison and comprehension.
Converting Decimals to Percentages
A percentage is a part of a whole expressed in hundredths. In other words, it is a value out of 100. For example, 93% means 93 out of 100, or .
The Formula
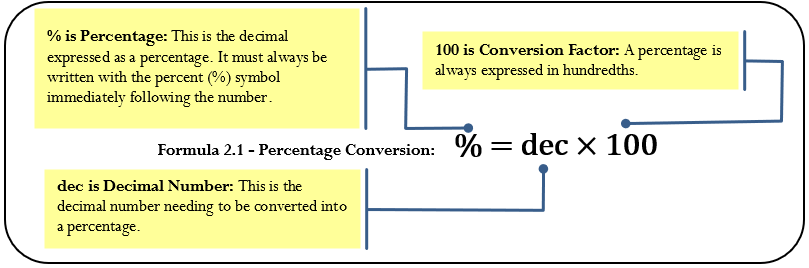
How It Works
Assume you want to convert the decimal number 0.0875 into a percentage. This number represents the dec variable in the formula. Substitute into Formula 2.1:
% = 0.0875 × 100 = 8.75%
Important Notes
You can also solve this formula for the decimal number. To convert any percentage back into its decimal form, you need to perform a mathematical opposite. Since a percentage is a result of multiplying by 100, the mathematical opposite is achieved by dividing by 100. Therefore, to convert 81% back into decimal form, you take 81% ÷ 100 = 0.81.
Things To Watch Out For
Your Texas Instruments BAII Plus calculator has a % key that can be used to convert any percentage number into its decimal format. For example, if you press 81 and then %, your calculator displays 0.81.
While this function works well when dealing with a single percentage, it causes problems when your math problem involves multiple percentages. For example, try keying 4% + 3% = into the calculator using the % key. This should be the same as 0.04 + 0.03 = 0.07. Notice, however, that your calculator has 0.0412 on the display.
Why is this? As a business calculator, you BAII Plus is programmed to take portions of a whole. When you key 3% into the calculator, it takes 3% of the first number keyed in, which was 4%. As a formula, the calculator sees 4% + (3% × 4%). This works out to 0.04 + 0.0012 = 0.0412.
To prevent this from happening, your best course of action is not to use the % key on your calculator. It is best to key all percentages as decimal numbers whenever possible, thus eliminating any chance that the % key takes a portion of your whole. Throughout this textbook, all percentages are converted to decimals before calculations take place.
Paths To Success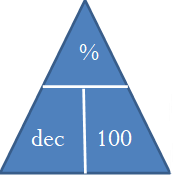
When working with percentages, you can use some tricks for remembering the formula and moving the decimal point.
Remembering the Formula. When an equation involves only multiplication of all terms on one side with an isolated solution on the other side, use a mnemonic called the triangle technique. In this technique, draw a triangle with a horizontal line through its middle. Above the line goes the solution, and below the line, separated by vertical lines, goes each of the terms involved in the multiplication. The figure to the right shows how Formula 2.1 would be drawn using the triangle technique.
To use this triangle, identify the unknown variable, which you then calculate from the other variables in the triangle:
- Anything on the same line gets multiplied together. If solving for %, then the other variables are on the same line and multiplied as dec × 100.
- Any pair of items with one above the other is treated like a fraction and divided. If solving for dec, then the other variables are above/below each other and are divided as
.
Moving the Decimal. Another easy way to work with percentages is to remember that multiplying or dividing by 100 moves the decimal over two places.
- If you are multiplying by 100, the decimal position moves two positions to the right.

- If you are dividing by 100, the decimal position moves two positions to the left (see Figure 2.5).


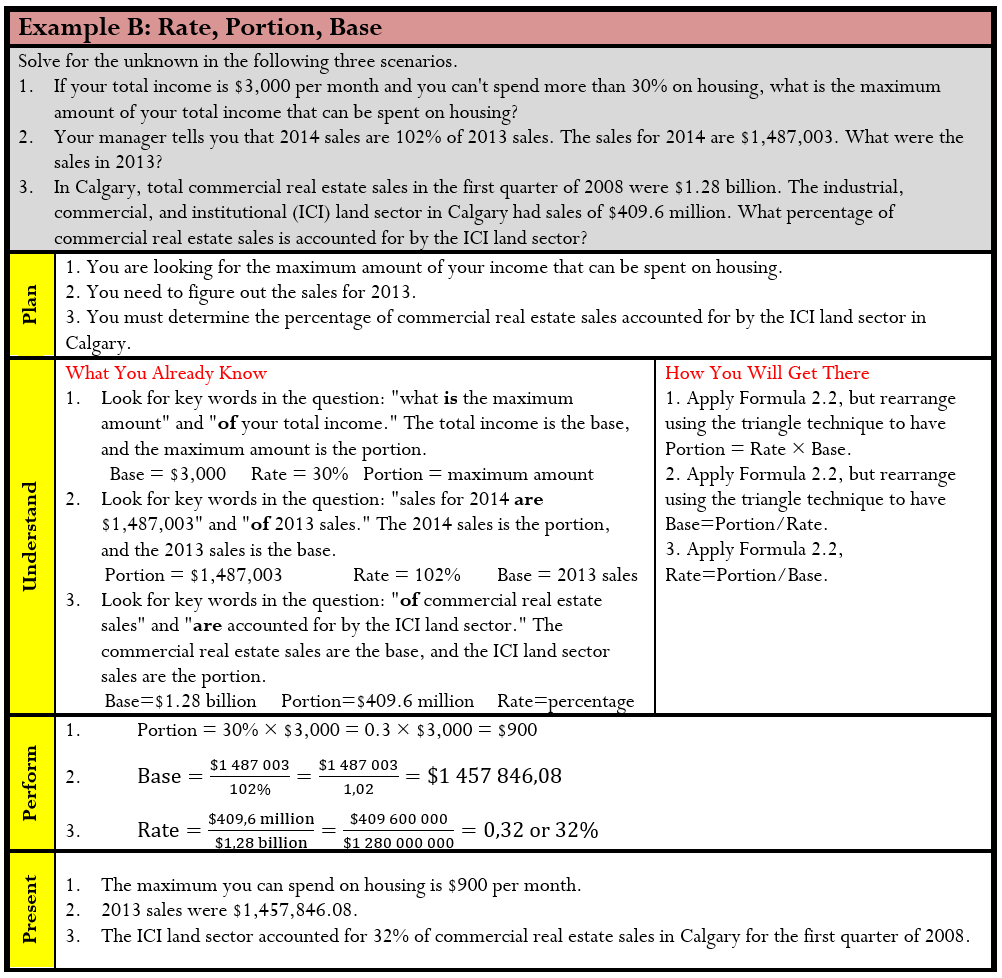
Rate, Portion, Base
In your personal life and career, you will often need to either calculate or compare various quantities involving fractions. For example, if your income is $3,000 per month and you can’t spend more than 30% on housing, what is your maximum housing dollar amount? Or perhaps your manager tells you that this year’s sales of $1,487,003 are 102% of last year’s sales. What were your sales last year?
The Formula
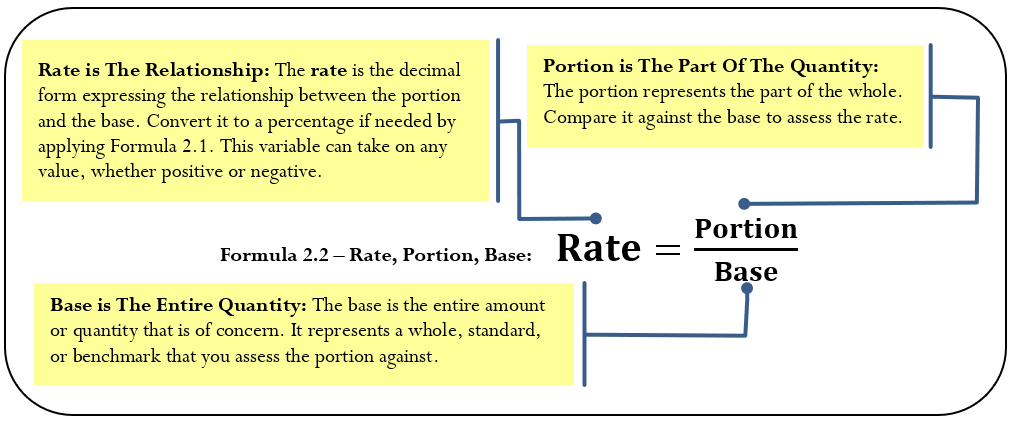
How It Works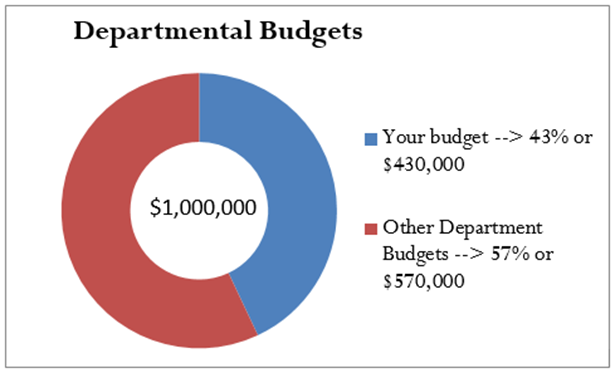
Assume that your company has set a budget of $1,000,000. This is the entire amount of the budget and represents your base. Your department gets $430,000 of the budget—this is your department’s part of the whole and represents the portion. You want to know the relationship between your budget and the company’s budget. In other words, you are looking for the rate.
- Apply Formula 2.2, where rate
.
- Your budget is 0.43, or 43%, of the company’s budget.
Important Notes
There are three parts to this formula. Mistakes commonly occur through incorrect assignment of a quantity to its associated variable. The table below provides some tips and clue words to help you make the correct assignment.

Things To Watch Out For
In resolving the rate, you must express all numbers in the same units—you cannot have apples and oranges in the same sequence of calculations. In the above example, both the company’s budget and the departmental budget are in the units of dollars. Alternatively, you would not be able to calculate the rate if you had a base expressed in kilometres and a portion expressed in metres. Before you perform the rate calculation, express both in kilometres or both in metres.
Paths To Success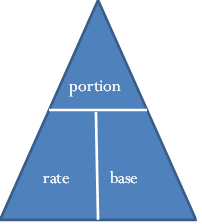
Formula 2.2 is another formula you can use the triangle technique for. You do not need to memorize multiple versions of the formula for each of the variables. The triangle appears to the right.
Be very careful when performing operations involving rates, particularly in summing or averaging rates.
Summing Rates. Summing rates requires each rate to be a part of the same whole or base. If Bob has 5% of the kilometres travelled and Sheila has 6% of the oranges, these are not part of the same whole and cannot be added. If you did, what does the 11% represent? The result has no interpretation. However, if there are 100 oranges of which Bob has 5% and Sheila has 6%, the rates can be added and you can say that in total they have 11% of the oranges.
Averaging Rates. Simple averaging of rates requires each rate to be a measure of the same variable with the same base. If 36% of your customers are female and 54% have high income, the average of 45% is meaningless since each rate measures a different variable. Recall that earlier in this chapter you achieved 68% on your test and Sandhu scored 70%. However, your test involved 19 questions and Sandhu’s involved 23 questions. These rates also cannot be simply averaged to 69% on the reasoning that (68% + 70%) / 2 = 69%, since the bases are not the same. When two variables measure the same characteristic but have different bases (such as the math quizzes), you must use a weighted-average technique.
When can you average rates? Hypothetically, assume Sandhu achieved his 70% by writing the same test with 19 questions. Since both rates measure the same variable and have the same base, the simple average of 69% is now calculable.
Give It Some Thought
Consider the following situations and select the best answer without performing any calculations.
- If the rate is 0.25%, in comparison to the base the portion is
- just a little bit smaller than the base.
- a lot smaller than the base.
- just a little bit bigger than the base.
- a lot bigger than the base.
- If the portion is $44,931 and the base is $30,000, the rate is
- smaller than 100%.
- equal to 100%.
- larger than 100% but less than 200%.
- larger than 200%.
- If the rate is 75% and the portion is $50,000, the base is
- smaller than $50,000.
- larger than $50,000.
- the same as the portion and equal to $50,000.
Click to Reveal Solutions:
- b (0.25% is 0.0025, resulting in a very small portion)
- c (the portion is larger than the base, but not twice as large)
- b (the portion represents 75% of the base, meaning the base must be larger)
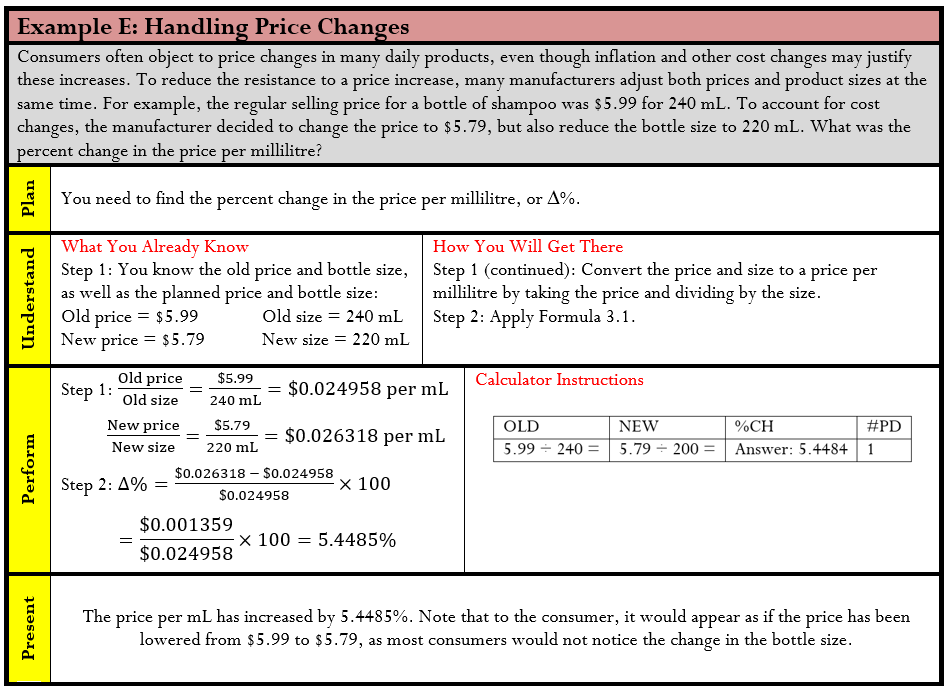
Percent Change
On your way to work, you notice that the price of gasoline is about 10% higher than it was last month. At the office, reports indicate that input costs are down 5.4% and sales are up 3.6% over last year. Your boss asks you to analyze the year-over-year change in industry sales and submit a report. During your coffee break, you look through the day’s e-flyers in your inbox. Home Depot is advertising that all garden furniture is 40% off this week; Safeway’s ad says that Tuesday is 10% off day; and a Globe and Mail story informs you that the cost of living has risen by 3% since last year. You then log in to your financial services account, where you are happy to find that the mutual funds in your RRSP are up 6.7% from last year. What are you going to do with all this information?
Understanding how data changes from one period to the next is a critical business skill. It allows for quick assessment as to whether matters are improving or getting worse. It also allows for easy comparison of changes in different types of data over time. In this section, the concept of percent change is explored, which allows for the calculation of change between two points in time. Then a rate of change over time is introduced, which allows you to determine the change per period when multiple points in time are involved in the calculation.
Percent Change
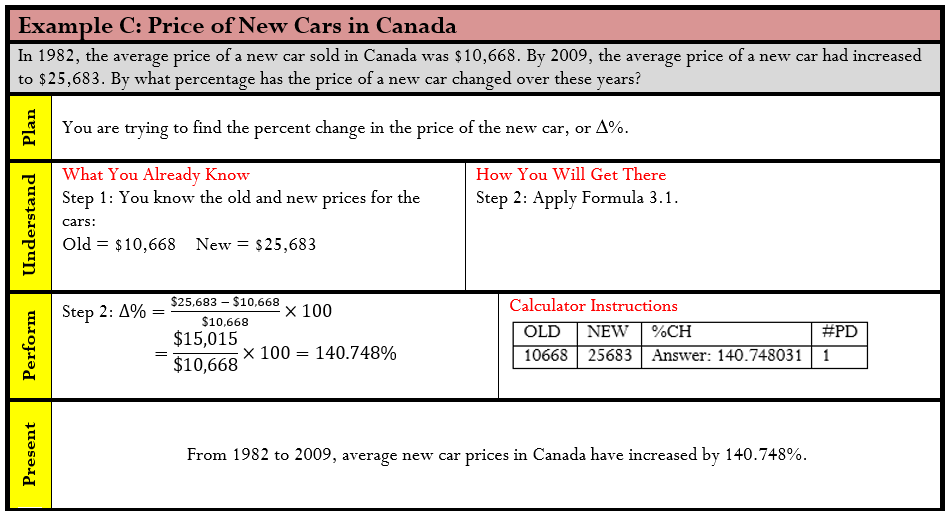
It can be difficult to understand a change when it is expressed in absolute terms. Can you tell at a glance how good a deal it is to buy a $359 futon for $215.40? It can also be difficult to understand a change when it is expressed as a percentage of its end result. Are you getting a good deal if that $215.40 futon is 60% of the regular price? What most people do find easier to understand is a change expressed as a percentage of its starting amount. Are you getting a good deal if that $359 futon is on sale at 40% off? A percent change expresses in percentage form how much any quantity changes from a starting period to an ending period.
The Formula
To calculate the percent change in a variable, you need to know the starting number and the ending number. Once you know these, Formula 3.1 (on the next page) represents how to express the change as a percentage.
Remember two critical concepts about percent change:
- Do Not Include the Original Quantity in the Change. Percent change represents the changes in the quantities, not the values of the quantities themselves. The original quantity does not count toward the percent change. Therefore, if any quantity doubles, its percent change is 100%, not 200%. For example, if the old quantity was 25 and the new quantity is 50, note that the quantity has doubled. However, 25 of the final 50 comes from the original amount and therefore does not count toward the change. We subtract it out of the numerator through calculating 50 − 25 = 25. Therefore, the change as a percentage is
The same applies to a tripling of quantity. If our new quantity is 75 (which is triple the old quantity of 25), then
The original value of 25 is once again subtracted out of the numerator. The original 100% is always removed from the formula. - Negative Changes. A negative change must be expressed with a negative sign or equivalent wording. For example, if the old quantity was 20 and the new quantity is 15, this is a decrease of 5, or a change of 15 − 20 = −5. The percent change is
Be careful in expressing a negative percent change. There are two correct ways to do this properly:- “The change is −25%.”
- “It has decreased by 25%.”
Note in the second statement that the word “decreased” replaces the negative sign. To avoid confusion, do not combine the negative sign with the word “decreased”—recall that two negatives make a positive, so “It has decreased by −25%” would actually mean the quantity has increased by 25%.

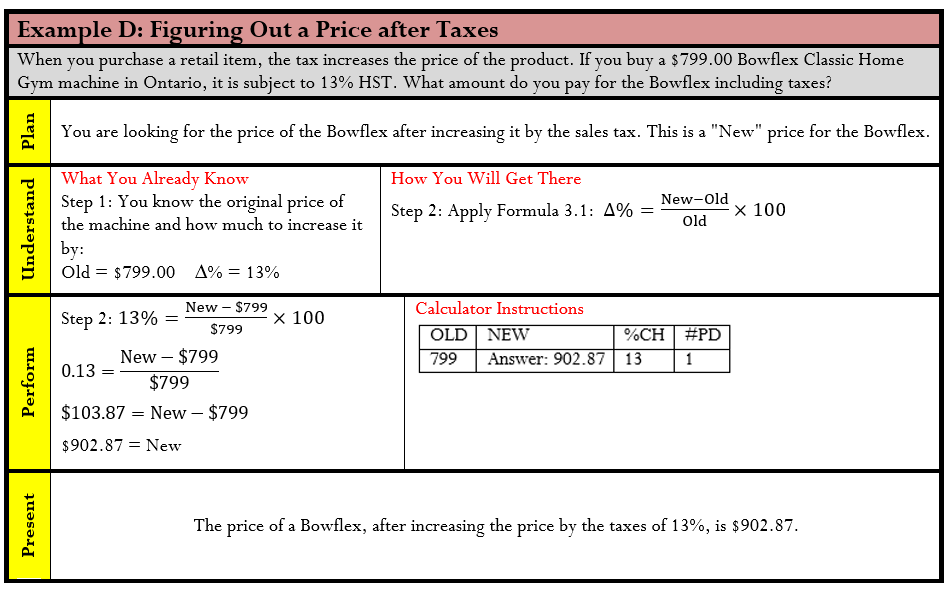
To solve any question about percent change, follow these steps:
Step 1: Notice that there are three variables in the formula. Identify the two known variables and the one unknown variable.
Step 2: Solve for the unknown variable using Formula 3.1.
Step 1: The known variables are Old = $10,000 and New = $15,000. The unknown variable is percent change, or ∆%.
Step 2: Using Formula 3.1,
Observe that the change in sales is +$5,000 month-over-month. Relative to sales of $10,000 last month, this month’s sales have risen by 50%.
Important Notes
To access the percent change function on your BAII Plus calculator, press 2nd ∆% located above the number 5 on your keypad. Always clear the memory of any previous question by pressing 2nd CLR Work once the function is open. Use the ↑ and ↓ arrows to scroll through the four lines of this function. To solve for an unknown variable, key in three of the four variables and then press Enter. With the unknown variable on your display, press CPT. Each variable in the calculator is as follows:
- OLD = The old or original quantity; the number that represents the starting point
- NEW = The new or current quantity; the number to compare against the starting point
- %CH = The percent change, or ∆% in its percent format without the % sign
- #PD = Number of consecutive periods for change. By default, it is set to 1. For now, do not touch this variable. Later in this section, when we cover rate of change over time, this variable will be explained.
Things To Watch Out For
Watch out for two common difficulties involving percent changes.
- Rates versus Percent Changes.
Sometimes you may be confused about whether questions involve rates or percent changes. Recall that a rate expresses the relationship between a portion and a base. Look for some key identifiers, such as “is/are” (the portion) and “of” (the base). For percent change, key identifiers are “by” or “than.” For example, “x has increased by y%” and “x is y% more than last year” both represent a percent change. - Mathematical Operations.
You may imagine that you are supposed to add or subtract percent changes, but you cannot do this. Remember that percentages come from fractions. According to the rules of algebra, you can add or subtract fractions only if they share the same base (denominator). For example, if an investment increases in value in the first year by 10% and then declines in the second year by 6%, this is not an overall increase of 10% − 6% = 4%. Why? If you originally had $100, an increase of 10% (which is $100 × 10% = $10) results in $110 at the end of the first year. You must calculate the 6% decline in the second year using the $110 balance, not the original $100. This is a decline of $110 × (−6%) = −$6.60, resulting in a final balance of $103.40. Overall, the percent change is 3.4%.
Paths To Success
A percent change extends the rate, portion, and base calculations introduced in Section 2.3. The primary difference lies in the portion. Instead of the portion being a part of a whole, the portion represents the change of the whole. Putting the two formulas side by side, you can calculate the rate using either approach.
Give It Some Thought
- It has been five years since Juan went shopping for a new car. On his first visit to a car lot, he had sticker shock when he realized that new car prices had risen by about 20%. What does this situation involve?
- Percent change
- Rate, portion, base
- Manuel had his home custom built in 2006 for $300,000. In 2014 he had it professionally appraised at $440,000. He wants to figure out how much his home has appreciated. How would he do so?
- The 2006 price is the “New,” and the 2014 price is the “Old.”
- The 2006 price is the “Old,” and the 2014 price is the “New.”
Click to Reveal Solutions:
-
- a (the question involves how car prices have changed; note the key word “by”)
- b (the 2006 price is what the house used to be worth, which is the old quantity; the 2014 price represents the new value of the home)
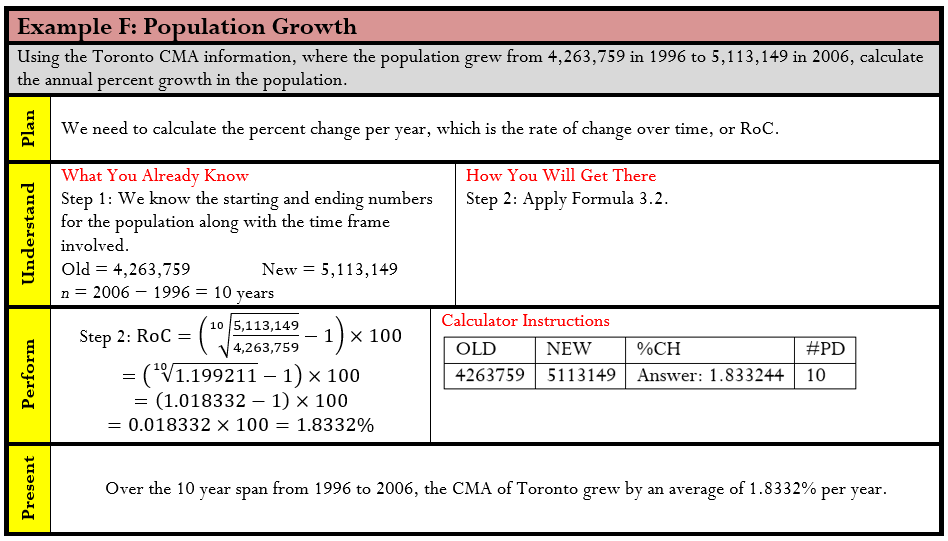
Rate of Change over Time
The percent change measures the change in a variable from start to end overall. It is based on the assumption that only a single change occurs. What happens when the ending number results from multiple changes and you want to know the typical value of each change? For example, the population of the Toronto census metropolitan area (CMA) has grown from 4,263,759 in 1996 to 5,113,149 in 2006. What annual percentage growth in population does this reflect? Notice that we are not interested in calculating the change in population over the 10 years; instead we want to determine the percentage change in each of the 10 years. The rate of change over time measures the percent change in a variable per time period.
The Formula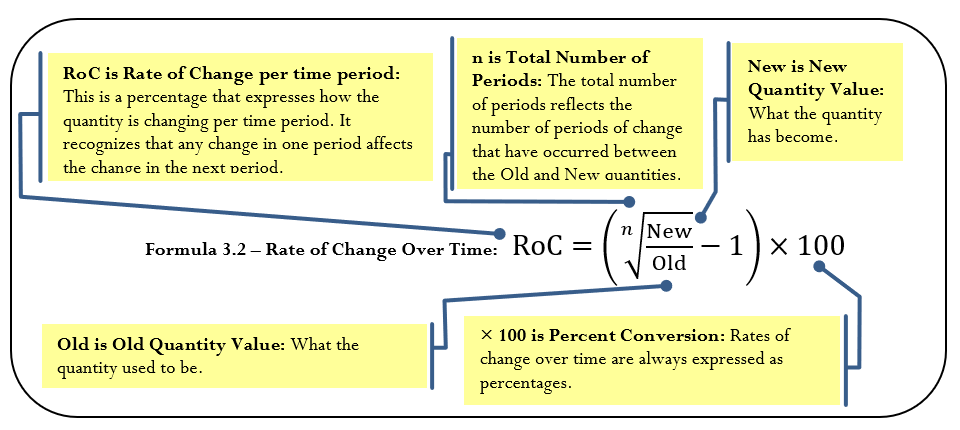
Calculating the rate of change over time is not as simple as dividing the percent change by the number of time periods involved, because you must consider the change for each time period relative to a different starting quantity. For example, in the Toronto census example, the percent change from 1996 to 1997 is based on the original population size of 4,263,759. However, the percent change from 1997 to 1998 is based on the new population figure for 1997. Thus, even if the same number of people were added to the city in both years, the percent change in the second year is smaller because the population base became larger after the first year. As a result, when you need the percent change per time period, you must use Formula 3.2.
When you work with any rate of change over time, follow these steps:
Step 1: Identify the three known variables and the one unknown variable.
Step 2: Solve for the unknown variable using Formula 3.2.
Important Notes
On your calculator, calculate the rate of change over time using the percent change (∆%) function. Previously, we had ignored the #PD variable in the function and it was always assigned a value of 1. In rate of change, this variable is the same as n in our equation. Therefore, if our question involved 10 changes, such as the annual population change of the Toronto CMA from 1996 to 2006, then this variable is set to 10.
Paths To Success
You may find it difficult to choose which formula to use: percent change or rate of change over time. To distinguish between the two, consider the following:
- If you are looking for the overall rate of change from beginning to end, you need to calculate the percent change.
- If you are looking for the rate of change per interval, you need to calculate the rate of change over time.
Ultimately, the percent change formula is a simplified version of the rate of change over time formula where n = 1. Thus you can solve any percent change question using Formula 3.2 instead of Formula 3.1.
Give It Some Thought
For each of the following, distinguish whether you should solve the question by the percent change formula or the rate of change over time formula.
- When Peewee started five-pin bowling with the Youth Bowling Canada (YBC) in 1997, his average was 53. In 2011, he finished his last year of the YBC with an average of 248. How did his average change from 1997 to 2011?
- A stock was priced at $4.34 per share in 2006 and reached $7.15 per share in 2012. What annual return did a shareholder realize?
- In 2004, total sales reached $1.2 million. By 2010, sales had climbed to $4.25 million. What is the growth in sales per year?
Click to Reveal Solutions:
- Percent change; looking for overall change
- Rate of change over time; looking for change per year
- Rate of change over time; looking for change per year

Personal Income Tax
You have just filled out your income tax return, where you see that your total payable for the year is more than $5,000. You are glad you do not have to pay this lump sum all at once! Instead, almost all of it has actually been paid already: Your employer has made regular deductions from each paycheque to cover your federal and provincial taxes.
In Canada, businesses are taxed differently than individuals and there are many nuances and complexities to address. For these reasons, this textbook does not cover business taxes, which require a course in corporate taxes.
For individuals, taxes are relatively straightforward. This section of the book uses the 2013 tax year federal and provincial/territorial personal income tax brackets to calculate the amount of these taxes that are ultimately deducted from your gross earnings. You can find current-year tax brackets at www.taxtips.ca/marginaltaxrates.htm.
Federal and Provincial/Territorial Tax Brackets and Tax Rates
Personal income tax is a tax on gross earnings levied by both the federal and provincial/territorial governments. All of Canada uses a progressive tax system in which the tax rate increases as the amount of income increases; however, the increased tax rates apply only to income amounts above minimum thresholds. Thus, higher income earners pay higher marginal tax rates than lower income earners. The format is similar to a graduated commission structure.
The federal and provincial/territorial governments offer a basic personal amount, which is the amount of income for which the wage earner is granted a tax exemption. In other words, it is tax-free income. This is designed to help low-income earners in Canada. Tax brackets are adjusted annually federally and in most provinces and territories to reflect increases in the cost of living, as measured by the consumer price index (CPI).
2013 Provincial Taxes
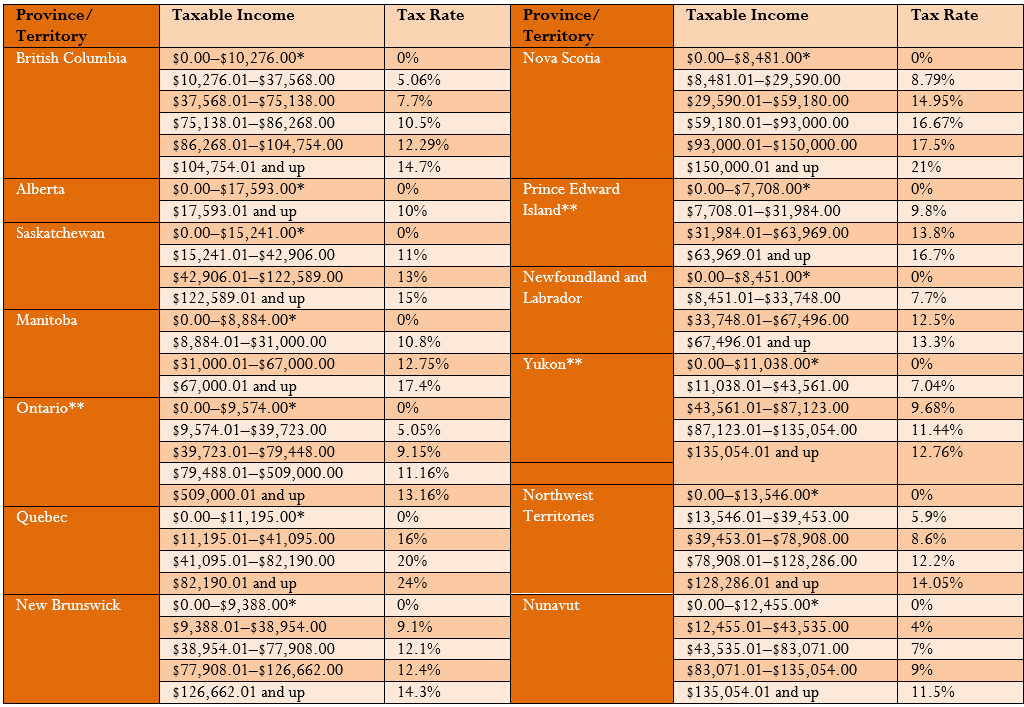 *These amounts represent the basic personal amount.
*These amounts represent the basic personal amount.
**There are additional income surtaxes in these provinces and Yukon. These surtaxes are not covered in this textbook.
2013 Federal Taxes
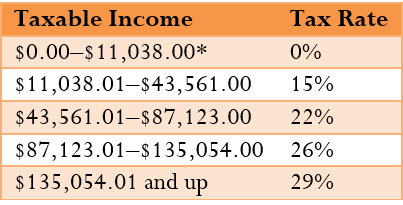
The Formula
To calculate the income taxes for any individual, you must total all taxes from all eligible gross earnings in every tax bracket. Formula 4.2 shows the calculation.

To calculate the total annual income tax owing in any tax year, follow these steps:
Step 1: Determine the total amount of gross earnings that are taxable for the individual.
Step 2: Calculate the federal income taxes owing. Using the federal tax table, split the gross earnings into each of the listed tax brackets, then calculate the taxes owing in each tax bracket by multiplying the income in the bracket and the tax rate. Round any tax amounts to two decimals.
Step 3: Calculate the provincial/territorial income taxes owing. Repeat the same process as in step 2, but use the appropriate tax brackets from the provincial tax table instead. Round any tax amounts to two decimals.
Step 4: Calculate the total annual income taxes owing by applying Formula 4.2. This means adding all calculated tax amounts from both steps 2 and 3 together.
Assume you live in British Columbia and your taxable gross income is $44,000. Here is how you would calculate your annual total federal and provincial taxes:
Step 1: The gross earnings are $44,000.
Step 2: Federally, your income falls into the first three brackets. Your first $11,038 is taxed at 0%; therefore, there are no income taxes on this amount. The next $32,523 (from $11,038.01 to $43,561.00) is taxed at 15%, thus $32,523 × 15% = $4,878.45. The last $439 (from $43,561.01 to $44,000.00) is taxed at 22%, thus $439 × 22% = $96.58.
Step 3: Provincially, your income falls into the first three brackets for British Columbia. Your first $10,276 is taxed at 0%; therefore, there are no income taxes on this amount. The next $27,292 (from $10,276.01 to $37,568.00) is taxed at 5.06%, thus $27,292 × 5.06% = $1,380.98. The last $6,432 (from $37,568.01 to $44,000) is taxed at 7.7%, thus $6,432 × 7.7% = $495.26.
Step 4: Your total federal income tax is $0.00 + $4,878.45 + $96.58 = $4,975.03. Your total provincial income tax is $0.00 + $1,380.98 + $495.26 = $1,876.24. Applying Formula 4.1, income tax = $4,975.03 + $1,876.24 = $6,851.27, which is the amount that will be deducted from total gross earnings.
Things To Watch Out For
Have you ever heard someone say, “I earn more income and moved to a higher tax bracket, so now I am earning less money and my paycheque is lower”? The progressive tax system used in Canada makes this statement untrue.
Remember that tax rates apply only to the portion of the gross earnings in the tax bracket and are not retroactive to lower levels of income. For example, if your taxable gross income increased from $80,000 to $88,000, your highest tax bracket is now 26% instead of 22%. However, your federal income tax is not calculated at 26% for your entire income. Rather, the first $11,038 is tax free, the next $32,523 is taxed at 15%, the next $43,562 is taxed at 22%, and the final $877 is taxed at 26%.
Paths To Success
It is sometimes beneficial to pre-calculate the total income taxes in any tax bracket under the assumption that the individual’s income comprises the entire tax bracket. This technique is particularly useful when repetitive calculations are required, such as determining the federal income taxes for each employee in an entire company. For example, the second federal tax bracket extends from $11,038.01 to $43,561, representing $32,523 of employee income. Since this bracket is taxed at 15%, someone who earns a higher income always owes the full amount of tax in this category, which is $32,523 × 15% = $4,878.45. The next tax bracket covers $43,561.01 to $87,123, representing $43,562 of income. Someone earning a higher income always owes the full amount of tax in this category, which is $43,562 × 22% = $9,583.64.
Assume taxable gross earnings of $88,000. With your pre-calculated income taxes in each bracket, you know the income taxes in the first three tax brackets are $0, $4,878.45, and $9,583.64, or $14,462.09 in total. You only need to calculate the tax on the portion of income in the final tax bracket of $877 × 26% = $228.02. The grand total is $14,462.09 + $228.02 = $14,690.11.


