6 Ratio and Proportion
Michael Hrycay
Section Information
Outcome/Competency: You will be able to apply ratios and proportion to trade specific problems.
Timing: 6h
Rationale: Why is it important for you to learn this skill?
If you go 100 km/hr down the highway, how far will you travel in 2 hours? Three hours? If you are going the same speed throughout, the answer is simple: 200 kilometers, and 300 kilometers. This is a basic example of ratio and proportion. Examples of ratio and proportion are found everywhere in life. Even things we have already learned in this course are examples of ratio and proportion such as fractions, percentages, and unit conversions! Understanding the math behind ratio and proportion will be useful in helping you predict quantities based on information you already know.
Objectives:
To be competent in this area, the individual must be able to:
- Identify a situation as proportional
- Model a situation using a proportion equation
- Solve a proportion equation and interpret the solution
Learning Goals
- Identify, write, and solve proportional equations and scenarios
Introduction:
This module will cover proportionality concepts and situations, ratios, equivalent ratios, and proportion equations. You will also learn how to find the missing factor in a proportion. You will be presented with content and examples and then given opportunities to do practice exercises.
Chapter Contents:
- Topic 1: Proportionality Concept and Situations
- Topic 2: Proportion Equation Scenarios
- Topic 3: Other Situations of Proportionality
- Test: Outcome 5
Topic 1: Proportionality Concept and Situations
1.1 Ratio
A ratio is an association between two or more quantities. There are many ways to describe a situation in terms of ratios. For example, look at this collection:
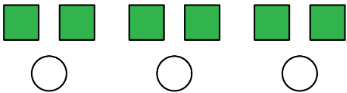
Here are some correct ways to describe the collection:
- The ratio of squares to circles is 6:3
- The ratio of circles to squares is 3 to 6.
Notice that the shapes can be arranged in equal groups, which allow us to describe the shapes using other numbers.
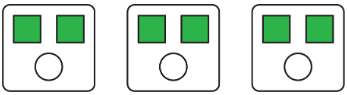
- There are 2 squares for every 1 circle.
- There is 1 circle for every 2 squares.
A ratio is an association between two or more quantities.
For example, the ratio 3:2 could describe a recipe that uses 3 cups of flour for every 2 eggs, or a boat that moves 3 meters every 2 seconds. One way to represent the ratio 3:2 is with a diagram that has 3 blue squares for every 2 green squares.
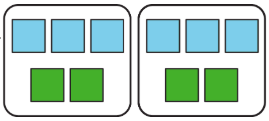
1.1 Practice Exercises
1.2 Equivalent Ratios
A recipe for fizzy juice says, “Mix 5 cups of cranberry juice with 2 cups of soda water.”
To double this recipe, we would use 10 cups of cranberry juice with 4 cups of soda water. To triple this recipe, we would use 15 cups of cranberry juice with 6 cups of soda water.
This diagram shows a single batch of the recipe, a double batch, and a triple batch:
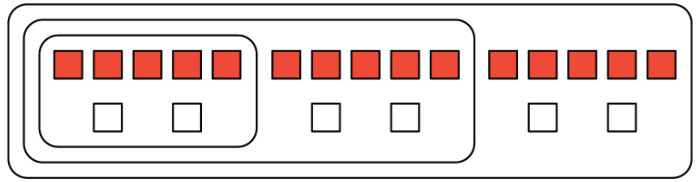
We say that the ratios 5:2, 10:4, and 15:6 are equivalent. Even though the amounts of each ingredient within a single, double, or triple batch are not the same, they would make fizzy juice that tastes the same.
Example 1
Here are diagrams representing three mixtures of powdered drink mix and water:
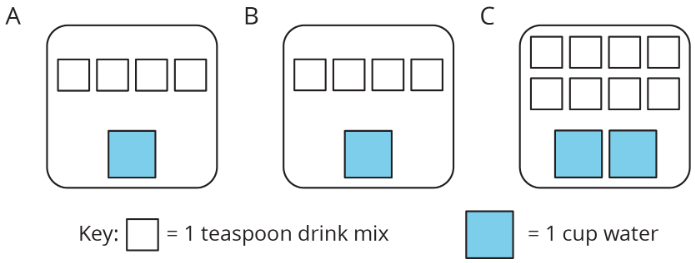
1. How would the taste of Mixture A compare to the taste of Mixture B?
2. Use the diagrams to complete each statement:
a) Mixture B uses cups of water and teaspoons of drink mix. The ratio of cups of water to teaspoons of drink mix in Mixture B is .
b) Mixture C uses cups of water and teaspoons of drink mix. The ratio of cups of water to teaspoons of drink mix in Mixture C is .
3. How would the taste of Mixture B compare to the taste of Mixture C?
Solution:
1. Same
2. a) 1, 4, 1:4
b) 1, 4, 1:4
3. Same, just more.
When mixing colors, doubling or tripling the amount of each color will create the same shade of the mixed color. In fact, you can always multiply the amount of each color by the same number to create a different amount of the same mixed color.
For example, a batch of dark orange paint uses 4 ml of red paint and 2 ml of yellow paint.
To make two batches of dark orange paint, we can mix 8 ml of red paint with 4 ml of yellow paint.
To make three batches of dark orange paint, we can mix 12 ml of red paint with 6 ml of yellow paint.
Here is a diagram that represents 1, 2, and 3 batches of this recipe.
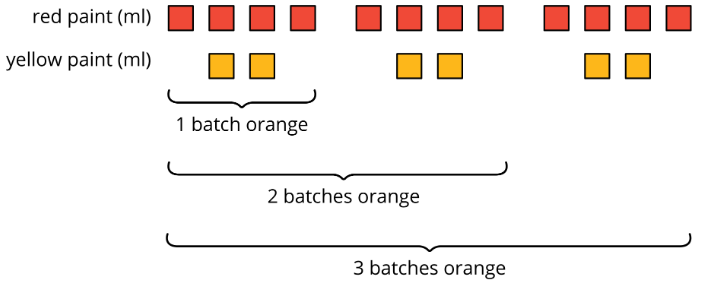
We say that the ratios 4:2, 8:4, and 12:6 are equivalent because they describe the same color mixture in different numbers of batches, and they make the same shade of orange.
Example 2
Diego makes green paint by mixing 10 tablespoons of yellow paint and 2 tablespoons of blue paint. Which of the following mixtures produce the same shade of green paint as Diego’s mixture?
a) For every 5 tablespoons of blue paint, mix in 1 tablespoon of yellow paint.
b) Mix tablespoons of blue paint and yellow paint in the ratio 1:5.
c) Mix tablespoons of yellow paint and blue paint in the ratio 15 to 3.
d) Mix 11 tablespoons of yellow paint and 3 tablespoons of blue paint.
e) For every tablespoon of blue paint, mix in 5 tablespoons of yellow paint.
Solution:
B, C, E
The recipe for Perfect Purple Water says, “Mix 8 mL of blue water with 3 mL of red water.”
Jada mixes 24 mL of blue water with 9 mL of red water. Andre mixes 16 mL of blue water with 9 mL of red water.
Which person will get a color mixture that is the same shade as Perfect Purple Water? Explain or show your reasoning.
Solution:
Jada is combining 3 times as much red and 3 times as much blue which is an equivalent ratio to the recipe. Andre is combining 2 times as much red and 3 times as much blue which is not an equivalent ratio to the recipe. Jada will get the same color mixture.
Summary: Ratio and Equivalent Ratios
All ratios that are equivalent to a:b can be made by multiplying both a and b by the same number.
For example, the ratio 18:12 is equivalent to 9:6 because both 9 and 6 are multiplied by the same number: 2.
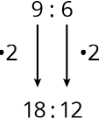
3:2 is also equivalent to 9:6, because both 9 and 6 are multiplied by the same number.
Is 18:15 equivalent to 9:6?
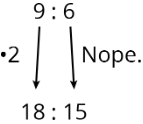
No, because 18 is 9 X 2, but 15 is not 6 X 2.
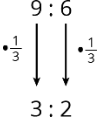
Two ratios are equivalent if you can multiply or divide each of the numbers in the first ratio by the same factor to get the numbers in the second ratio. For example, 8:6 is equivalent to 4:3, because 8 ÷ 2 = 4 and 6 ÷ 2 = 3.
A recipe for lemonade says to use 8 cups of water and 6 lemons. If we use 4 cups of water and 3 lemons, it will make half as much lemonade. Both recipes taste the same, because and are equivalent ratios.
Example 4
Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a diagram that shows why they are equivalent ratios.
4:5 and 8:10
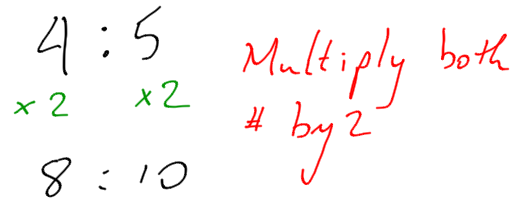
18:6 and 6:2
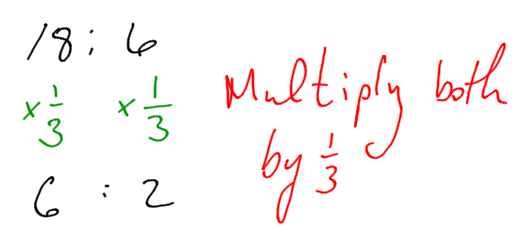
Example 5
Explain why 6:4 and 18:8 are not equivalent ratios.
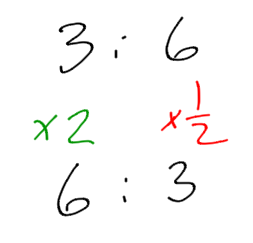
These are not equivalent because they are not multiplied by the same numbers.
1.3 Rates
Suppose a train traveled 100 meters in 5 seconds at a constant speed. To find its speed in meters per second, we can find a unit rate. A unit rate is a ratio of distance (in this case) to one second. This can be found by dividing the numbers.
100 meters : 5 seconds
100 divided by 5 is 20.
100 meters : 5 seconds is equivalent to 20 meters:1 second. The unit rate of speed of the train is 20 meters per second, or 20 m/s.
Glossary for Rates:
Definition: Meters per Second
Meters per second is a unit for measuring speed. It tells us how many meters an object goes in one second. For example, a person walking 3 meters per second is going faster than another person walking 2 meters per second.
Definition: Per
The word per means “for each.” For example, if the price is $5 per ticket, that means you will pay $5 for each ticket. Buying 4 tickets would cost $20, because 4 x 5 = 20.
Definition: Unit Price
The unit price is the cost for one item or for one unit of measure. For example, if 10 feet of chain link fencing cost $150, then the unit price is 150 ÷ 10, or $15 per foot.
Example 6
A cargo ship traveled 150 nautical miles in 6 hours at a constant speed. How far did the cargo ship travel in one hour?
Solution:
Calculate a unit rate of speed by dividing.
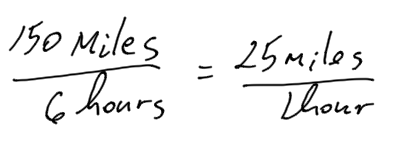
Example 7
John ran 10 meters in 2.7 seconds. Melodi ran 10 meters in 2.4 seconds.
Who ran faster? Explain how you know.
At this rate, how long would it take each person to run 50 meters? Explain or show your reasoning.
Solution:
We can reason that if Melodi ran the same distance, but took less time, she must be the faster runner.
Mathematically, we can find the unit rate for each runner.
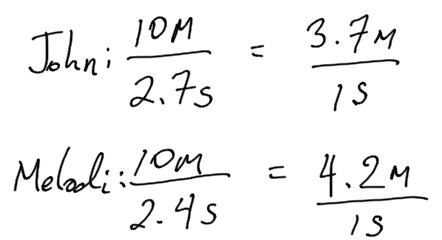 Melodi has the higher unit rate (or speed.)
Melodi has the higher unit rate (or speed.)
Sometimes we want to know whether two situations are described by the same rate. To do that, we can write an equivalent ratio for one or both situations so that one part of their ratios has the same value. Then we can compare the other part of the ratios.
The other option is to divide the two values to find a unit rate, and compare the unit rates.
Example 8
A scooter travels 30 feet in 2 seconds at a constant speed.
- What is the speed of the scooter in feet per second?
- A skateboard travels 55 feet in 4 seconds. Is the skateboard going faster, slower, or the same speed as the scooter?
Solution:
1. Divide to find the unit rate:
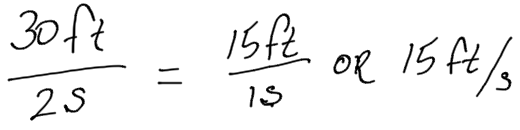
2. Find the unit rate of the skateboarder
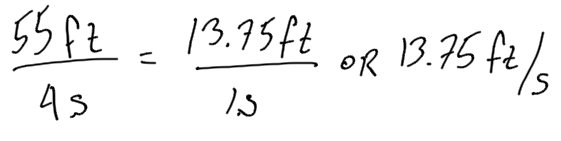 The skateboarder has a smaller unit rate than the scooter, so the skateboarder is going slower.
The skateboarder has a smaller unit rate than the scooter, so the skateboarder is going slower.
Practice Exercises: Proportionality Concept and Situations
1. A slug travels 3 centimeters in 3 seconds. A snail travels 6 centimeters in 6 seconds. Both travel at constant speeds. “The snail was traveling faster because it went a greater distance.” Do you agree with this statement? Explain or show your reasoning.
2. If you blend 2 scoops of chocolate ice cream with 1 cup of milk, you get a milkshake with a stronger chocolate flavor than if you blended 3 scoops of chocolate ice cream with 2 cups of milk. Explain or show why.
3. There are 2 mixtures of light purple paint. Which mixture is a lighter shade of purple? Explain your reasoning.
Mixture A is made with 5 cups of purple paint and 2 cups of white paint.
Mixture B is made with 15 cups of purple paint and 8 cups of white paint.
Solution:
1. No, even though snail went further and it took longer, their speeds are the same: 1 cm/s.
2. Compare unit rate of mixture 1 (2 scoops: 1 cup) and mixture 2 (3 scoops: 2 cups or 1.5 scoops: 1cups). In the first mixture, there is more chocolate per cup of milk. It is the stronger flavored milk shake.
3. Compare the unit rates.
Mixture A
Mixture B
Mixture B is a lighter shade because it has less purple paint per cup of white.
Topic 2: Proportion Equation and Scenarios
To solve problems about something happening at the same rate, we often need:
- Two pieces of information that allow us to write a ratio that describes the situation.
- A third piece of information that gives us one number of an equivalent ratio. Solving the problem often involves finding the other number in the equivalent ratio.
Example 1
Suppose we are making a large batch of juice and the recipe says, “Mix 5 cups of cranberry juice with 2 cups of soda water.” We know that the ratio of cranberry juice to soda water is 5:2. As in the example with the distance travelled by the train, we can divide to find how many cups of cranberry juice are required for one cup of water. 5 divided by 2 is 2.5. So, 2 and a half cups of cranberry juice is required for one cup of water. This is the unit rate.
We still need to know something about the size of the large batch. If we use 16 cups of soda water, what number goes with 16 to make a ratio that is equivalent to 5:2?
To make this large batch taste the same as the original recipe, once we have the unit rate, we can multiply by the number of cups of water to fund the required cups of cranberry juice. 2.5 x 16 = 40. we would need to use 40 cups of cranberry juice.
This data can be stored in a table. Tables are useful when you have a rate, but don’t want to do a calculation for every scenario. You can look up the pre calculated values in the table.
|
|
|
|
cranberry juice (cups) |
soda water (cups) |
|
1 |
2.5 |
|
2 |
5 |
|
3 |
7 |
|
4 |
10 |
|
… |
… |
|
16 |
40 |
For each row of the table, the number on the left is multiplied by 2.5 to obtain the number on the right. We can keep adding rows until we reach the values we are looking for.
Glossary for Proportion Equation and Scenarios
Definition: Table
A table organizes information into horizontal rows and vertical columns. The first row or column usually tells what the numbers represent. For example, here is a table showing the tail lengths of three different pets. This table has four rows and two columns.
|
pet |
tail length (inches) |
|
dog |
22 |
|
cat |
12 |
|
mouse |
2 |
Practice Exercises
1. Create a table: A car has a gas consumption of 9 L to 100 km.
a) What will the two columns be titled?
b) Create 5 rows for values 100 km, 200 km, …, 500 km.
c) Calculate the gas consumption for each row.
Solution:
|
Kilometers |
Gas Consumption |
|
100 |
9 |
|
200 |
18 |
|
300 |
27 |
|
400 |
36 |
|
500 |
45 |
2.1 Ratios, Rates, and Proportions From a Mathematical Perspective
Tables can be useful in certain situations, but be cumbersome. Another more direct way to find a number in a proportion is to use algebra to solve a proportion equation.
A proportion is a statement that two ratios or rates are equal. The following two examples show how to read proportions.

2.2 Finding the Missing Factor in a Proportion
Many practical problems can be solved by writing the given information as proportions. Such proportions will be composed of three specified numbers and one unknown number. It is customary to let a letter, such as x, represent the unknown number. An example of such a proportion is
x/4 = 20/16
This proportion is read as ” x is to 4 as 20 is to 16.”
There is a method of solving these proportions that is based on the equality of fractions. Remember, 2 fractions are equivalent if you can multiply (or divide) the same number to top and bottom to obtain the new fraction. Another way to tell if 2 fractions are equivalent is if their cross products are equal. For example,
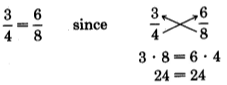
Notice that in a proportion that contains three specified numbers and a letter representing an unknown quantity, that regardless of where the letter appears, you can find the unknown value.
The missing factor in a proportion can be determined by dividing the product by the known factor, that is, if x represents the missing factor, then
x = (product) ÷ (known factor)
A way to remember this might be this diagram:
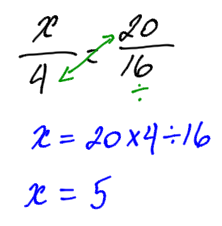 Cross-multiply the two numbers that are diagonally opposite and divide by the third number
Cross-multiply the two numbers that are diagonally opposite and divide by the third number
What is actually happening, using algebra, is this:
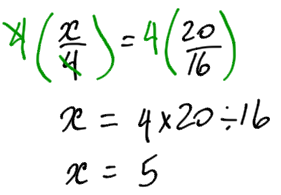
But only when you have a proportion equation, you can take the shortcut above.
Example 1
![]() =
= ![]() (Find the cross-product)
(Find the cross-product)
16x = 3 × 64
16x = 192 (Divide 192 by 16)
x = 12
The means that
16 : 3 = 64 : 12 or, 16 is to 3 as 64 is to 12.
Example 2
![]() =
= ![]() (Find the cross-product)
(Find the cross-product)
8x = 9 × 40
8x = 360 (Divide 360 by 8)
x = 45
The means that
9 : 8 = 45 : 40 or, 9 is to 8 as 45 is to 40.
2.3 Writing the proportion equation
When setting up a proportion equation, you must have the same units on the top of both sides of the equation, and the same units on the bottom of each side of the equation.
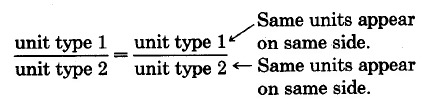
Both cross products produce a statement of the type:
(unit type 1) x (unit type 2) = (unit type 1) x (unit type 2)
However, if we write the same type of units on different sides, such as,
(unit type 1) / (unit type 2) = (unit type 2) / (unit type 1)
We can see that this is an incorrect comparison by observing the following example: It is incorrect to write:
2 hooks/ 3 poles = 6 poles / 4 hooks
for two reasons.
- The cross product is numerically wrong: (2 x 4 ≠ 3 x 6)
- The cross product produces the statement “hooks are to hooks as poles are to poles,” which makes no sense.
2.3 Practice Exercises: Proportion Equation and Scenarios
A. For the following 8 problems solve each proportion.
B. For the following 5 problems, express each sentence as a proportion then solve the proportion
- 5 hats are to 4 coats as x hats are to 24 coats
- x cushions are to 2 sofas as 24 cushions are to 16 sofas.
- 1 spacecraft is to 7 astronauts as 5 spacecraft are to x astronauts.
- 56 microchips are to x circuit boards as 168 microchips are to 3 circuit boards.
- 18 calculators are to 90 calculators as x students are to 150 students.
- x dollars are to $40,000 as 2 sacks are to 1 sack.
C. Indicate whether the proportion is true or false
- 3/16 = 12/64
- 2/15 = 10/75
- 1/9 = 3/30
- 6 knives/7 forks = 15 forks/12 knives
- 33 miles/1 gallon = 99 miles/3 gallons
- 320 feet/5 seconds = 65 feet/1 second
D. Practice
- A caterer needs to buy 21 pounds of pasta to cater a wedding. At a local store, 8 pounds of pasta cost $12. How much will the caterer pay for the pasta there? Write a ratio for the given information about the cost of pasta and find the answer.
- Lin is reading a 47-page book. She read the first 20 pages in 35 minutes. If she continues to read at the same rate, will she be able to complete this book in under 1 hour? If so, how much time will she have left? If not, how much more time is needed?
- Diego can type 140 words in 4 minutes. At this rate, how long will it take him to type 385 words? How many words can he type in 15 minutes?
Solution:
Part A
- 2
- 7
- 8
- 20
- 8
- 35
- 27
- 3
Part B
- 5/4 = x/24, x=30
- x/2 = 24/16, x=3
- 1/7 = 5/x, x=35
- 56/x = 168/3, x=1
- 18/90 = x/150, x=30
- x/40000 = 2/1, x=80000
Part C
- T,
- T
- F
- Proportion improper
- T
- F
Part D
- $12/8 lbs = x/21 lbs, x=31.50. It will cost $31.50.
- 35 min/20 pages = x/47 pages, x= 82.25. It will take 82 minutes to finish the book. It won’t be done in under 1 hour. She will need 22 more minutes.
- 4 min/140 words = x min/385 words, x = 11. It will take 11 minutes to write 385 words. 4 min/140 words = 15 min/x words, x=525. He can type 525 words in 15 minutes.
Topic 3: Other Situations of Proportionality
There are so many situations where the proportion equation in math is useful, although we may not have realized we were using it. Here are some of them.
3.1 Percentages
The word percent actually comes from two words “per” and “cent.” From a previous section, the word “per” means “for every.” The word “cent” means, in French, one hundred. (Remember, when we still had pennies, they were called cents, and one hundred of the made up one dollar.) The word “percent” literally means “for every one hundred.”
In order to find a percentage, we usually just divide. For example, the statement “7 out of 10 dentists recommend using toothpaste” means that 70 percent of dentists recommend using toothpaste.
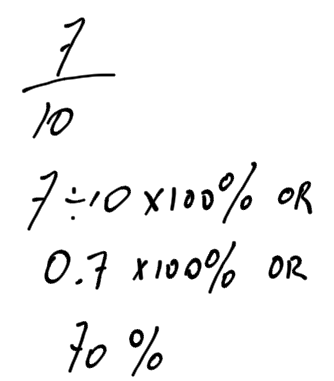
What is really happening, with the proportion equation is:
7/10 = x/100
If 7 out of 10 dentists recommend using toothpaste, then how many out of 100 recommend using toothpaste?
Using our short-cut from before:
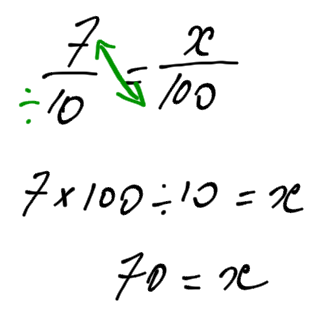
3.2 Unit Conversions
A conversion factor can be considered a rate. For example, there are 25.4 millimetres in one inch. This can be expressed as:
25.4mm : 1inch
If we want to convert inches to millimetres, we can use the proportion equation where one side is the conversion rate.
Example 1
Convert 37.627 inches into millimetres.
Set up the proportion equation. Remember to keep the same units on top of each side, and the same units on the bottom of each side. (Note, however, that it doesn’t matter if the inches appear on the top of the equation or the bottom of the equation, so long as both sides are the same.)
25.4 millimetres/1 inch = x millimetres/37.627 inches
Using our short cut from before:
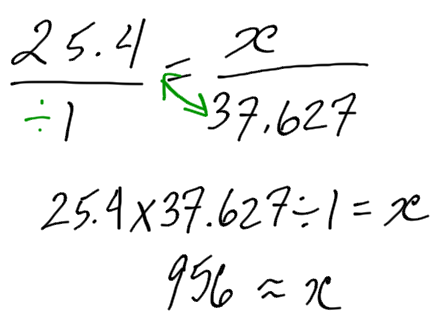
There are roughly 956 millimetres in 37.627 inches.
Here are a couple of things to note:
- Generally, round the answer to the nearest whole number when measuring in millimetres. It is impossible to measure less than a millimeter on a standard ruler.
- When you have a unit rate (25.4 millimetres per one inch) it is cumbersome to use the proportion equation. You would normally just multiply 25.4 X 37.627.
3.3 Similar Triangles
If a triangle has been expanded, the sides are in proportion. (What expanded means in this case is like zooming into a picture on your cell phone. The picture looks the same, only bigger.)
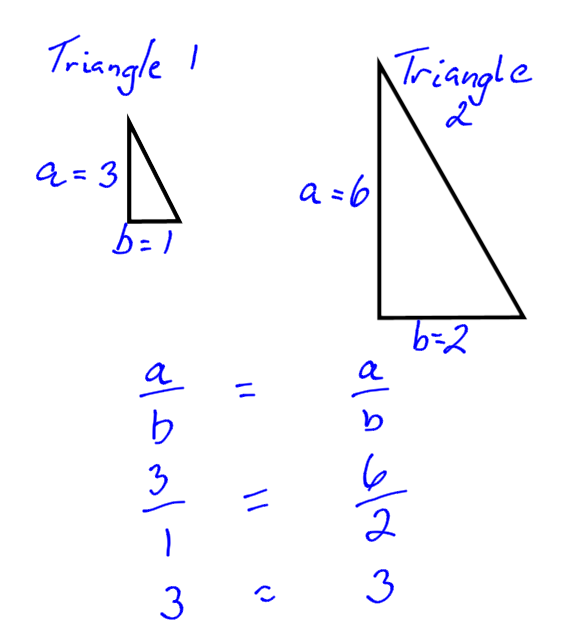
So, when we have two triangles that are similar, we can use the proportion equation to find the unknown side.
Example 2
Find the unknown side.
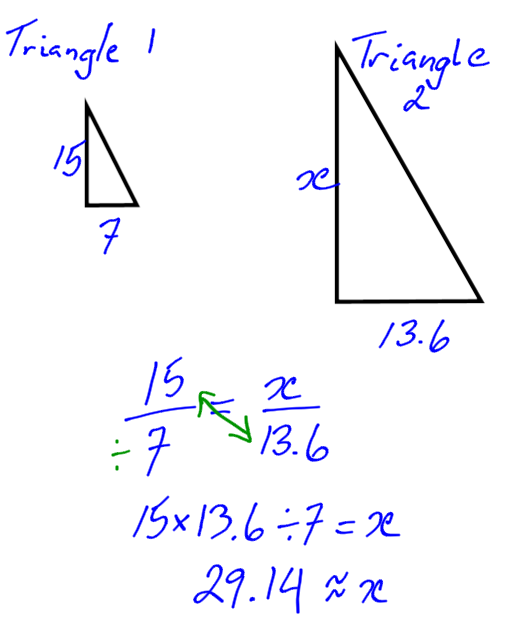
The unknown side is approximately 29.14. This will come up again in the trigonometry chapter.
3.1 – 3.3 Practice Exercises: Other Situations of Proportionality
- A student received 37 out of 48 on an exam. What percent did the student achieve?
- The ratio of pounds to kilograms is 2.2 lbs to every 1 kg. Convert 74.8 lbs to kg.
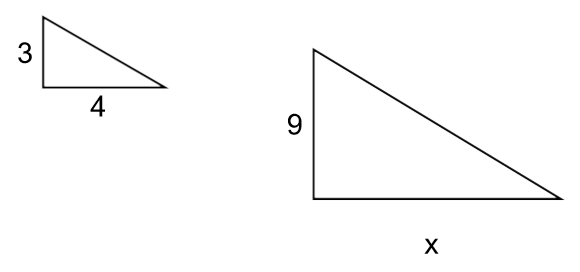
- The following two triangles are similar (they have the same angles). Find the unknown side.
Solution:
- 37/48 = x/100, x=77%
- 2.2 lbs/1 kg = 74.8 lbs/x, x=34
- 3/4 = 9/x, x=12
Learning Task: Outcome 5 Test
Complete the Essentials 1 Math: Ratios and Proportion Chapter Quiz on Brightspace.
Attributions
This information has been extracted and modified from at Basic Math (Illustrative Mathematics – Grade 6). (2020, June 11). Retrieved August 5, 2021, from https://math.libretexts.org/@go/page/35040
This is licensed under CC BY .
This content may be downloaded for free at Basic Math (Illustrative Mathematics – Grade 6). from https://math.libretexts.org/@go/page/35040
This information has been extracted and modified from: Denny Burzynski, Wade Ellis, Fundamentals of Mathematics. OpenStax CNX. Jul 29, 2013 http://cnx.org/contents/5de5485b-b230-4665-a39a-a500f1d0924d@4.6.

