Introduction

Ratio and Proportion are the basis of most of the math you will do as a carpenter.  Even though you may not think about certain problems in terms of ratio and proportion, these problems can be expressed using proportion.  The following sections will demonstrate this.

Topics

• Mixtures
• Simplifying Fractions
• The Proportion Equation
• Rates
• Unit Conversions
• Percent
• Similar Triangles
• Roof Slope
• Stairs

Mixtures

A good way to explain ratios and proportion is to give the example of mixtures.

If you are mixing a bowl of punch for a party of 7 people, a recipe might be:

1 can fruit juice and 1 bottle of sprite.

If 14 people are coming to the party, you need twice as much punch.  You need twice as much fruit juice, and twice as much sprite.  The doubled recipe would be:

2 cans of fruit juice and 2 bottles of sprite.

The ratio of fruit juice to sprite can be written as:

1 can fruit juice : 1 bottle of sprite

The ratio can also be represented as a fraction:

Practice Exercises:

In each of the scenarios, write the appropriate ratio.

a) Make lemonade with 6 cups of water for every 8 large lemons

b) Mix 2 parts blue to 3 parts yellow to make green paint.

c) For a quick and balanced trail mix, combine 3 parts nuts, 2 parts dried fruit, and 2 parts dark chocolate chips.

d) The ratio of cement to sand to stone in concrete with a compressive strength of 2500 psi is 1 to 2 to 4. How much cement should you purchase if you have 6 kg of sand? How much stone?

Expanding and Reducing Fractions

We have learned, on a tape measure, that is the same as .

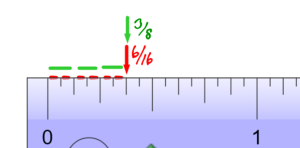
Mathematically, we can change  into  by multiplying top and bottom by 2.

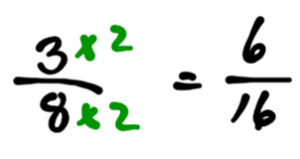
Just like when doubling the recipe for punch, we doubled the cans of fruit juice, and the cans of sprite.

Going the other direction, we can change  into by dividing top and bottom by 2.

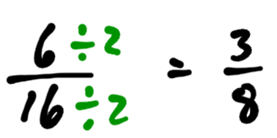
Practice Exercises

Practice reducing these fractions.  Divide top and bottom by the same number.

a)

b)

c)

d)

Practice expanding these fractions.  Fill in the space by multiplying or dividing top and bottom by the same number.

a)

b)

c)

d)

The Proportion Equation

In the previous section, we found the top or bottom number of a fraction by multiplying or dividing by a whole number.  We expanded the following fraction:

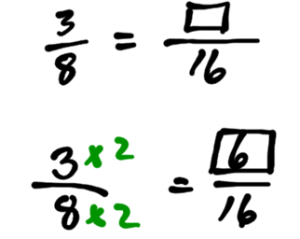
In some cases, it is difficult to find a number to multiply or divide by.  For example, reduce the following fraction:

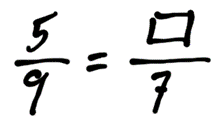
It is not easy to find a number to multiply 9 by, to get 7.  Rather than guessing for numbers, we can “solve” this proportion equation.  There is an easy way to do this: cross multiply and divide.

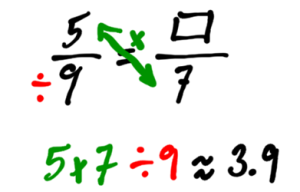
We have found that .

Practice Exercises

a)

b)

c)

d)

Rates

Another example of proportionality is a rate.  If someone travels at a rate of 100 kilometres per hour down the highway, then it makes sense that in 2 hours, they will travel 200 kilometres.  This is a statement of proportionality.

Notice that on the left side of the equation, the ratio is km on top, hours on the bottom.  This means that the right side must also have km on top and hours on the bottom.

Practice Exercises:

Set up and solve a proportion equation for each of the following scenarios:

a) 5 pounds of apples cost $14.95. How much were they per pound?

b) Gas costs $1.54/L. How much will you pay for 35 L?

c) If your resting heart rate is 65 bpm, how many times would you expect your heart to beat in an hour?

d) You are buying vinyl plank flooring for a cabin that is 860 ft2. One case contains 24.90 ft2. How many cases should you purchase?

e) *On a scaled drawing, a building measures 4.5 cm tall. If the scale of the drawing is 25 meters per 2 cm, how tall is the actual building?

Unit Conversions

Unit conversions are another example of ratio and proportion.  We know that millimetres relate to inches in a ratio of:

25.4 mm : 1 inch

This ratio can also be written in the form of a fraction:

Example

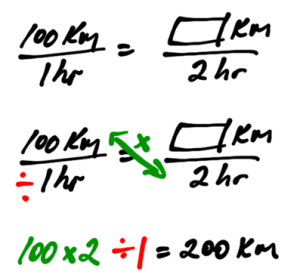
Convert 15.7 inches to millimetres.

Set up the following proportion equation:

Answer: 15.7 inches is approximately 399 millimetres.

Practice Exercises

Solve the following unit conversions using the proportion equation.

a) Convert 19.8 inches to mm

b) Convert 7524 mm to m

c) Convert 2.98 yards to feet

d) Convert 60 inches to feet

Percent

Percentages can be found using the proportion equation.  Remember, percent means per 100.  That is, a percentage is a rate per 100.

Example

If 23 out of 329 people drive a Honda car, what percentage of people drive a Honda car?

In this case, set up a proportion equation where the part (23) over the total (329) equals something over 100.  (Percent is per 100.)

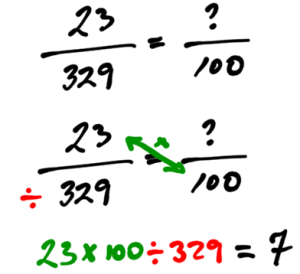
Answer: Roughly 7 percent of people drive a Honda car.

Example

A product is marked up by 80 percent.  The mark up amount (profit) is $683 dollars.  What is the original amount of the product?

In this case, the proportion equation looks backwards, but the process is the same.

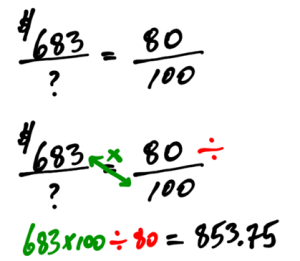
Answer: The original amount was $853.75.

Practice Exercises

Solve the following percentage situations using a proportion equation.

a) In the first 10 regular season games, Team Saskatchewan’s goalie stopped 328 of 350 shots. What is this hockey star’s save percentage?

b) 68% of students surveyed prefer Coke over Pepsi. If 220 students were surveyed, how many prefer Coke?

c) At 230 cm, the wingspan of a bald eagle is 163% of that of the red-tailed hawk. Based on this information, what is the average wingspan of a red-tailed hawk?

d) A painter has painted 45% of a long fence. If they have painted 70 m so far, how long is the entire fence?

e) Your current time for running a 5 km race is 36 minutes. If you can reduce your time by 5%, how many minutes faster will you be?

Similar Triangles

The basis of stairs and roofs are triangles.  A right angle triangle contains one 90 degree angle.  A pair of similar triangles have the same angles, but different length sides.

The following are similar triangles because all the angles are the same.  The approximate side lengths are listed.

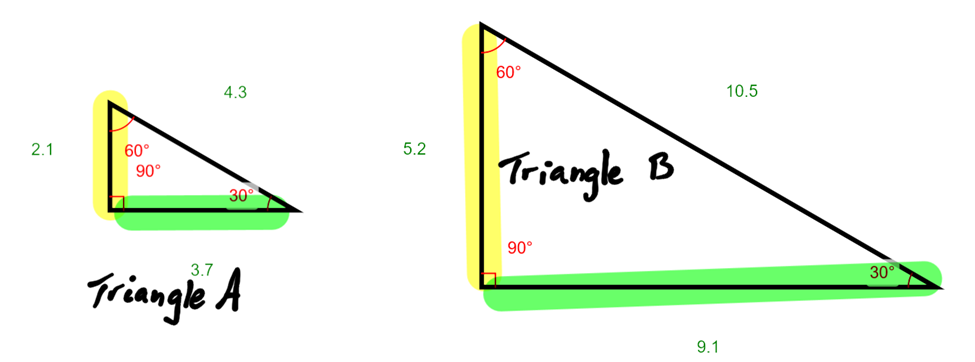
If you form a ratio of yellow side to green side of triangle A and compare it to the ratio of the yellow to green side of triangle B, you will find the sides are proportional. (Note, the decimal is only accurate to the nearest 10th because all the measurements are only given to the nearest 10th.)

Example

Find the unknown side of the pair of similar 90 degree triangles using the proportion equation.

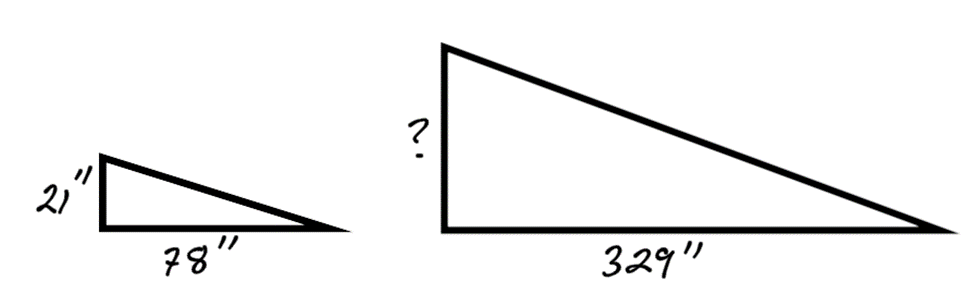
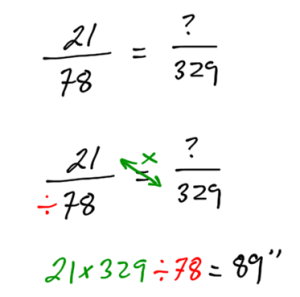
Answer: The unknown side is roughly 89 inches long.

Practice Exercises

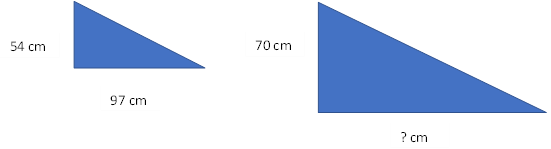
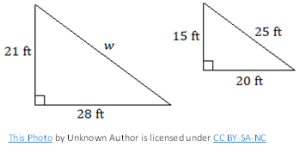
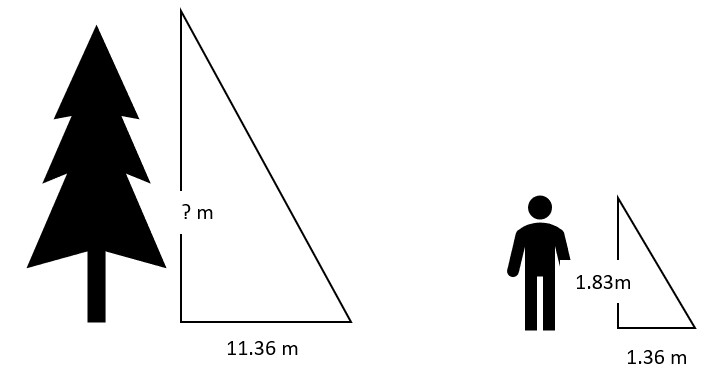
Find the unknown sides using the proportion equation. Round decimal answers to the nearest tenth.

a)

b)

c)

Roof Slope

A roof has what is called a “slope”.  The slope is a measure of how steep the roof is.  This can be represented by ratio.  The ratio is how far the roof goes up over how far the roof extends horizontally (side to side.)  The length the roof goes up is called the rise and the length the roof extends horizontally is called the run.  The span is the width of the building, so the total run of the roof as shown below is half the span.

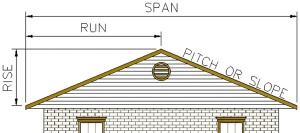
Source: https://www.roofcalc.org/roof-pitch/

You can imagine that a roof creates a triangle, which is useful because we can use similar triangles to calculate values as shown in the previous section.

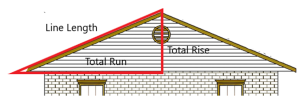
There are a few common slopes used for building roofs, but of course, each building has a different size.  From before, we know that the ratio of total run to total rise will be the same, no matter how big the triangle, if the triangles have the same slope.

Roof slope in carpentry is indicated by a small triangle called the unit triangle.  It is a “unit” triangle because it represents a ratio over 12” (1 foot) of run.  Common ratios are:

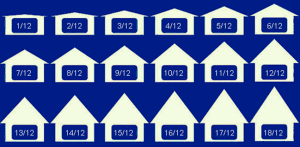
Source: https://www.greenawaltroofing.com/blog/2018/3/29/about-roof-pitch

The numbers give the rise, in inches, and the run, in inches.  Because these are unit triangles, the run is always 12 inches, or one foot.

Let’s put it together with an example.

Example

Consider a building that is 32 feet wide.  The slope of the roof is to be 4/12 (a common residential slope.)  This means for every 12 inches (one foot) of run, the roof will go up 4 inches.

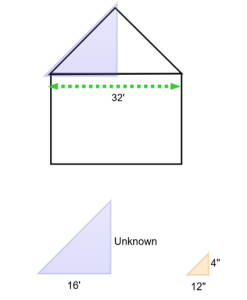
You can see there are two similar triangles.  The blue represents the whole roof, the orange represents the unit triangle.  They have the same slope, and we can use the proportion equation to determine the unknown total rise of the roof.

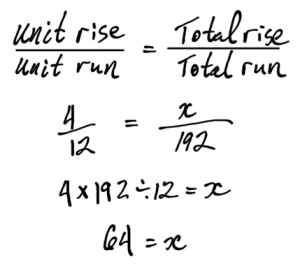
Answer: The total rise of the roof will be 64 inches, or 5’-4”.

Practice Exercises

a) The span of the building is 36’ and the roof slope will be 6/12. What is the total rise of the roof in inches?

b) The total rise of the roof is 6’-8” and the slope is 4/12. What is the span of the building?

c) The span of the garage roof is 26 feet and the total rise is 8’-8”. Which slope was used for the trusses?

Stairs

Stairs have a lot of similarity with roofs in terms of slope.  However, the unit slope of stairs is even easier to visualize.  The unit slope is the rise over run of one step in the staircase.

When talking about stairs, the unit rise is called the riser and the unit run is called the tread.  The total slope is called the line of flight, the total height of the staircase is called the total rise, and the total length of the staircase is called the total run.  Notice the large green triangle formed by the total rise, the total run, and the line of flight.

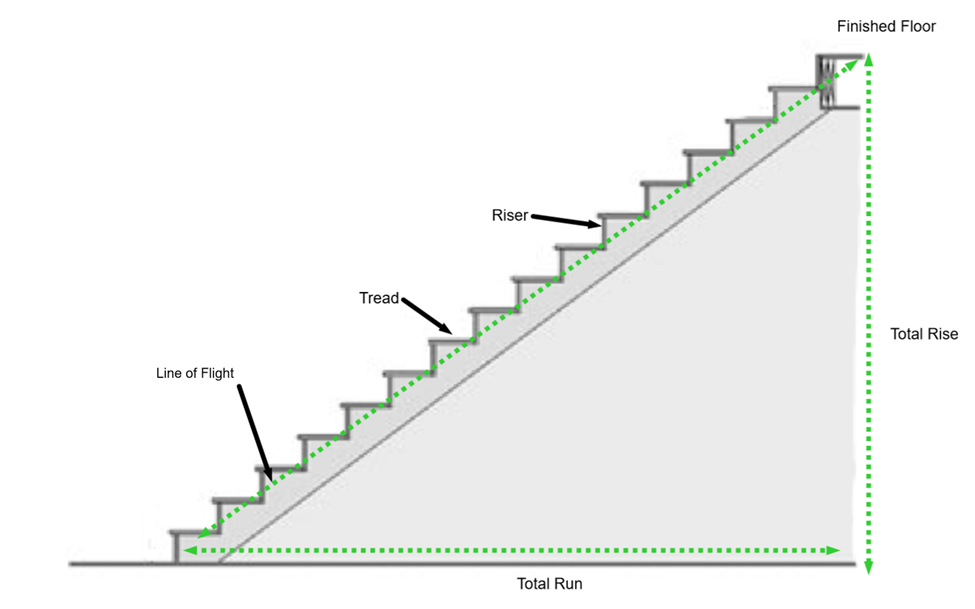
Each step represents a unit triangle.

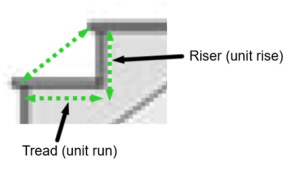
Example

The total rise of a staircase is 3.2 m, and the total run is 4.2 m.  This is often determined on a blueprint or by measuring.  The ideal height of a stair (riser) is 180 mm.  What would the tread depth be?

Consider the two similar triangles:

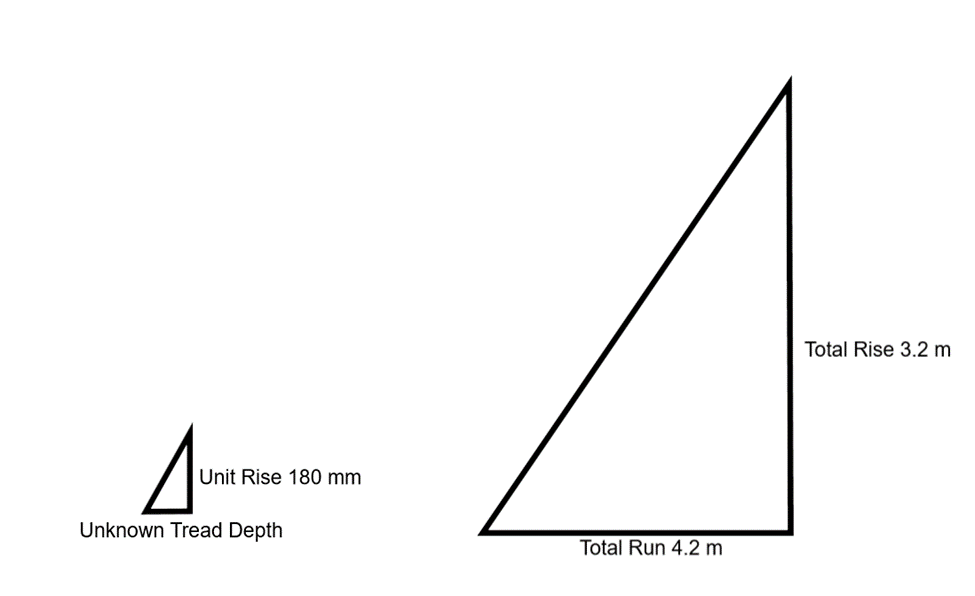
Use the proportion equation, but note that you need to change 180 mm to m to match other units:

Answer: The stairs should have a tread depth of 236 mm.

Practice Exercises

a) The total rise of a staircase is 2.7 m, and the total run is 3.25 m. The height of a stair (riser) is 188 mm. What would the tread depth be?

b) The total rise of a staircase is 1.19 m, and the total run is 1.53 m. The tread depth is 244 mm. What riser height was used?