28 Space and Shape
Michael Hrycay
Section Information
Outcome/Competency: You will be able to model and calculate scenarios in two- and three-dimensions using geometry.
Timing: 6h
Rationale: Why is it important for you to learn this skill?
Geometry is the study of shapes. Being able to calculate volume and area of a shape, for example, is very important in calculating supplies required for building. You will study shapes, and learn and apply calculations related to perimeter, circumference, area, surface area, volume, and Pythagoras’ Theorem in imperial and metric systems.
Objectives:
To be competent in this area, the individual must be able to:
- Demonstrate understanding of perimeter, area of 2-D shapes, and surface area and volume of 3-D objects including units in SI and Imperial systems of measurement
Learning Goals
- Model, calculate, interpret, and solve problems in two and three dimensions by using different representations and manipulating formulae
- Apply conversion factors using unit analysis and calculation to solve scenarios and situational problems
Introduction:
In this section you will learn about circumference, diameter, radius, area, surface area, and volume. You’ll be presented with concepts and examples, and given opportunities to practice throughout.
Chapter Contents:
- Topic 1: Perimeter and Circumference
- Topic 2: Area
- Topic 3: Surface Area
- Topic 4: Volume
- Topic 5: Pythagoras’ Theorem
- Test: Outcome 7
Shapes
| Circle:
A circle is a perfectly round shape with all points on its boundary equidistant from its center. |
 |
| Square:
A square is a four-sided shape where all sides are equal in length and all angles are right angles. |
 |
| Triangle:
A triangle is a shape with three sides and three angles.
A right triangle is a triangle with one angle measuring 90 degrees, called a right angle. |
  |
| Rectangle:
A rectangle is a four-sided shape with four right angles. Opposite sides of a rectangle are equal in length and parallel to each other. |
 |
Topic 1: Perimeter and Circumference
We can make use of conversion skills with denominate numbers to make measurements of geometric figures such as rectangles, triangles, and circles. To make these measurements we need to be familiar with several definitions.
1.1 Polygons
A polygon is a closed plane (flat) figure whose sides are line segments (portions of straight lines).
|
Polygons
|
Not polygons
|
1.2 Perimeter
The perimeter of a polygon is the distance around the polygon. To find the perimeter of a polygon, we simply add up the lengths of all the sides.
Example 1
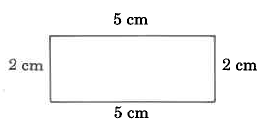
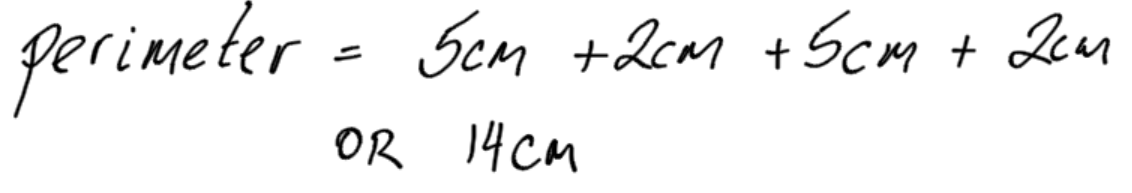
 Don’t be tempted to memorize a formula for this. Some people may think that they should memorize a formula such as: Perimeter = 2X length + 2 X width. This type of memorization is unnecessary if you simply remember the perimeter is the sum of all the sides.
Don’t be tempted to memorize a formula for this. Some people may think that they should memorize a formula such as: Perimeter = 2X length + 2 X width. This type of memorization is unnecessary if you simply remember the perimeter is the sum of all the sides.
Example 2
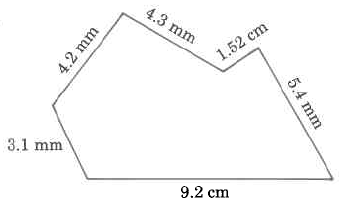
The sides do not need to be going perpendicular or parallel to each other. In this irregular shape, to find the perimeter, you still need to add all the sides.
 When adding measurements together, they must be in the same units. Notice some of the units are in mm, and some in cm. There are 10 mm in 1 cm.
When adding measurements together, they must be in the same units. Notice some of the units are in mm, and some in cm. There are 10 mm in 1 cm.

Example 3
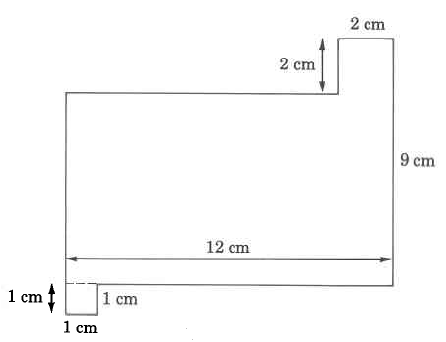
In some regular shapes you will need to figure out unknown measurements based on other given measurements. Find the sides labeled A, B and C.
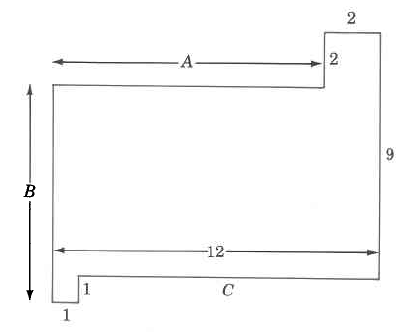
If the measurements you need are across the shape, it is sometimes useful to visualize them all together like in this diagram:
Consider side A:
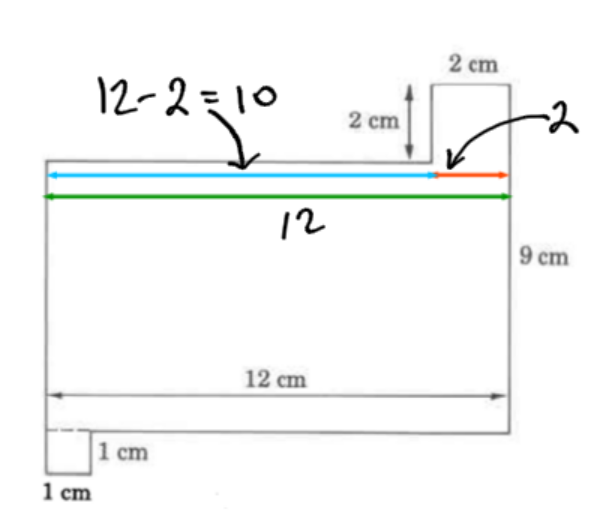
The unknown top side, A (blue), is 10 cm long.
Consider side B:
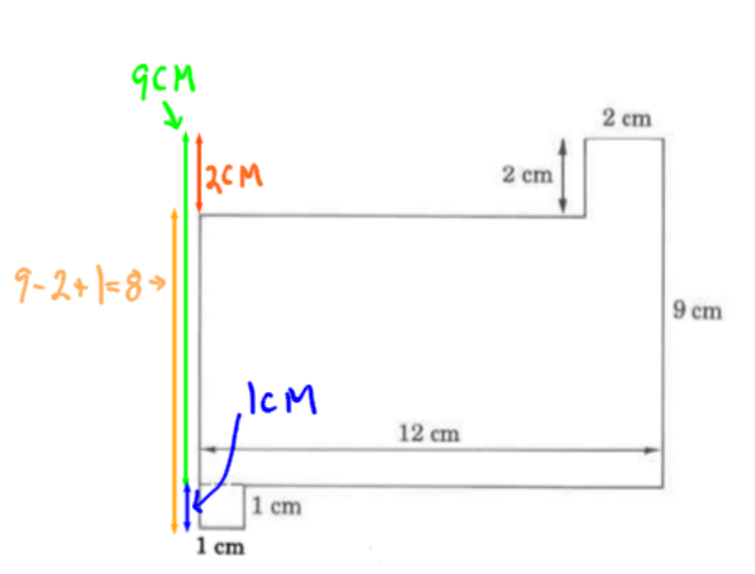
The unknown side B (yellow), is 8 cm.
Consider unknown side C:
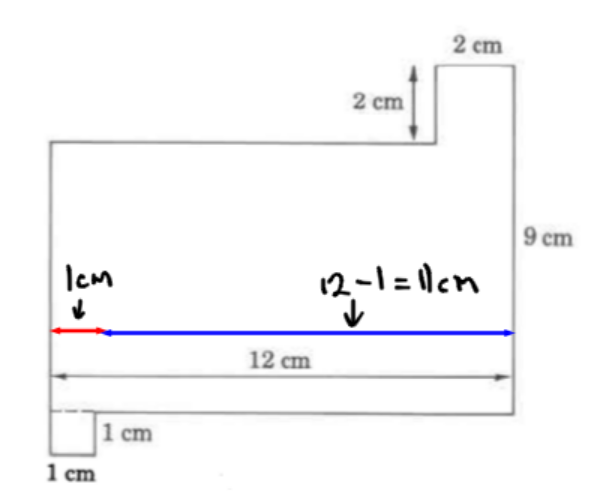
The unknown side, C (blue), is 11 cm long.
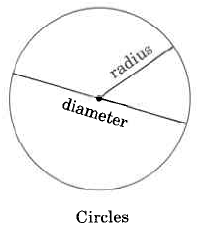
1.3 Circumference/Diameter/Radius
Circumference
The circumference of a circle is the distance around the circle. In plain language, the circumference is the perimeter of a circle.
You could measure the circumference of a circle with a string, but if you wanted to calculate the circumference, you need to use a formula. The formula depends upon one of two measurements: the diameter, or the radius.
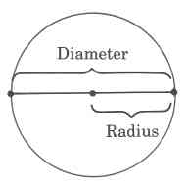
Diameter
A diameter of a circle is any line segment that passes through the center of the circle and has its endpoints on the circle.
Radius
A radius of a circle is any line segment having as its endpoints the center of the circle and a point on the circle. The radius is one half the diameter.
1.4 The Number π
The symbol π, read “pi,” represents the nonterminating, nonrepeating decimal number 3.14159 … . This number has been computed to millions of decimal places without the appearance of a repeating block of digits.
For computational purposes, π is often approximated as 3.14. We will write π≈3.14 to denote that π is approximately equal to 3.14. The symbol “≈” means “approximately equal to.”
When doing calculations on your calculator with a pi button you should use it, and round the answer after. Here is the pi button:

1.5 Circumference of a Circle
To find the circumference of a circle, we need only know its diameter or radius. We then use a formula for computing the circumference of the circle. Formulas are usually composed of letters that represent important, but possibly unknown, quantities.
C=2πr
OR
C=πD
Example 4
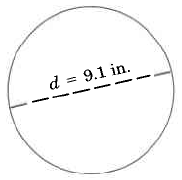
Find the circumference of the circle:
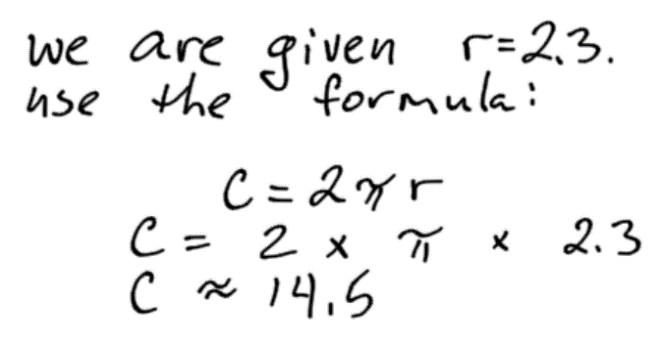
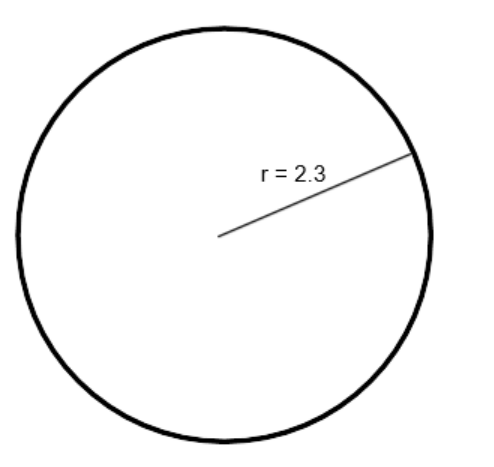
Example 5
Find the circumference of the circle:
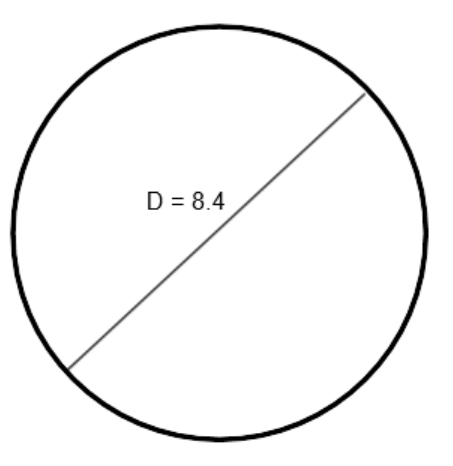
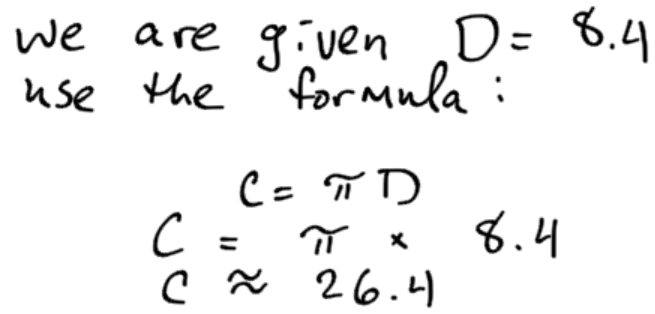
Practice Exercises: Perimeter and Circumference
- Find the perimeter of the shapes below:
a)
b)
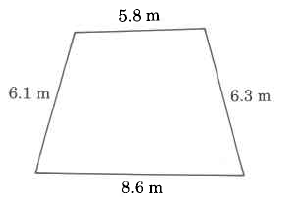
c)
d)
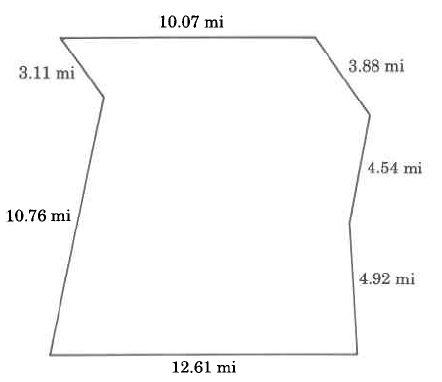
2. Extension Question: Find the perimeters of the following figures
a)
Questions for construction trades:
3. For the next questions, refer to this floor plan:
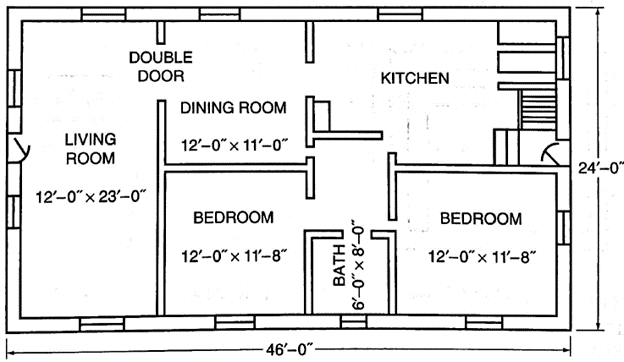
a) What is the perimeter of the living room in the plan shown? (Do not deduct for openings.)
b) What is the perimeter of the outside walls?
c) How many feet of baseboard are needed for the living room? (Deduct 3 feet for single door openings and 5 feet for double door openings.)
d) How many linear feet of shoe base are needed for the two bedrooms? (Deduct 3 feet for each door opening.)
e) How many linear feet of casing are needed for both sides of the double door between the dining room and the living room? (Allow 7 feet for each vertical piece and 5 feet 6 inches for each horizontal piece.
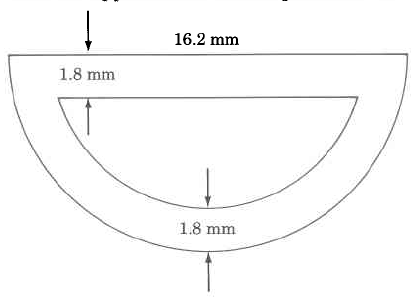
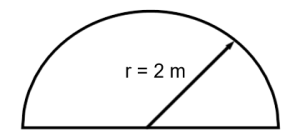
4. What is the perimeter of the semicircular form in the following figure? (Express your answer to the nearest thousandth of a metre.)
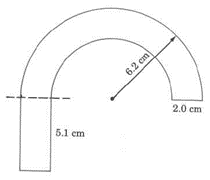
5. Find the perimeter
Solution:
1. a) 20 ft.
b) 26.8 m
c) 49.89 mi
d) 28.6 in
2. a) 74mm
3a. 70′, b. 140′, c. 62′, d. 88′-8″, e. 39′
4. 10.28 m
5. 46.87 cm
Topic 2: Area
The area of a surface is the amount of square length units contained in the surface.
For example, 3 sq in. means that 3 squares, 1 inch on each side, can be placed precisely on some surface. (The squares may have to be cut and rearranged so they match the shape of the surface.)

2.1 Finding Areas of Some Common Geometric Figures
We will examine the area of the following geometric figures:
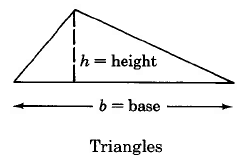
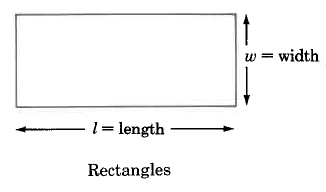
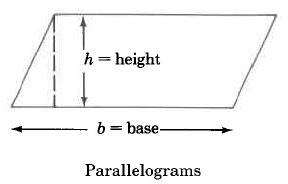
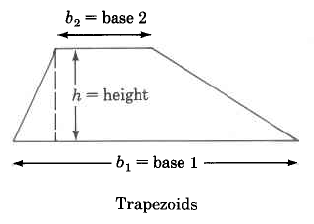
We can determine the areas of these geometric figures using the following formulas.
|
|
Figure |
Area Formula |
Statement |
|
|
Triangle |
|
Area of a triangle is one half the base times the height. |
|
|
Rectangle |
|
Area of a rectangle is the length times the width. |
|
|
Parallelogram |
|
Area of a parallelogram is base times the height. |
|
|
Trapezoid |
|
Area of a trapezoid is one half the sum of the two bases times the height. |
|
|
Circle |
|
Area of a circle is π times the square of the radius. |
 Remember, when calculating “one half” or “over two” the way to type that in the calculator is using the divide button. For example, “one half the base times the width” in your calculator is base × width ÷ 2.
Remember, when calculating “one half” or “over two” the way to type that in the calculator is using the divide button. For example, “one half the base times the width” in your calculator is base × width ÷ 2.Example 1
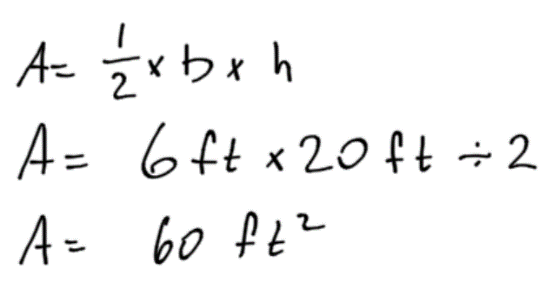
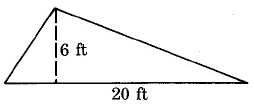
Note that feet multiplied by feet give ft2 pronounced as “feet squared.” (The unit is squared; this does not mean square the number.) Whenever a unit is squared, it is a unit of area.
Example 2
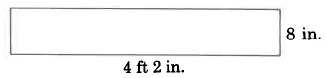
In this example, we need to convert 4 ft 2 in into units of inches. You cannot mix different units when finding area. There are 12 inches per foot.
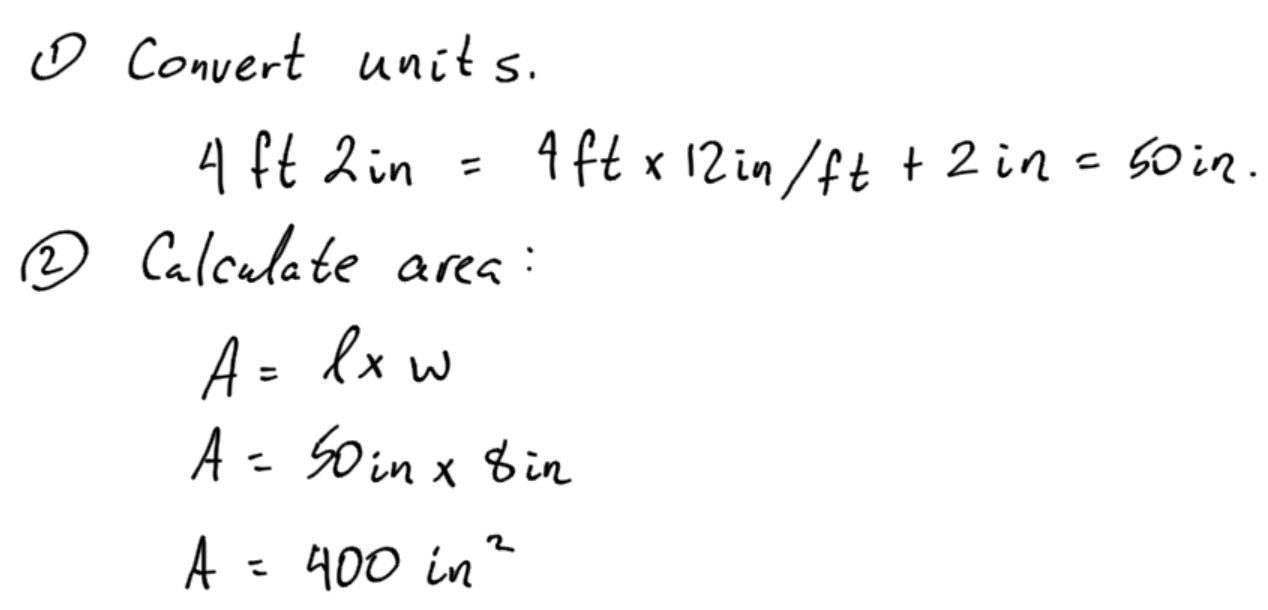
Example 3
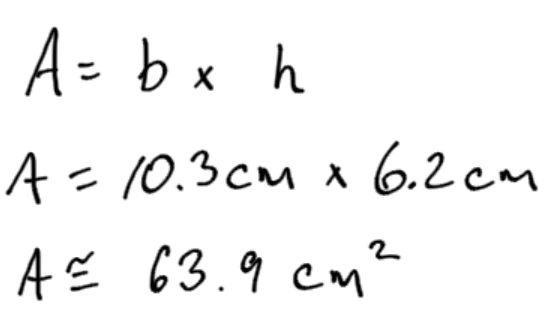
Example 4

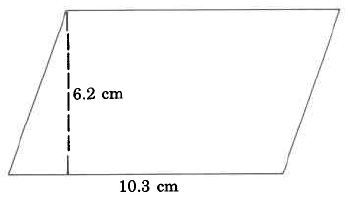
In this case, call the bottom b1 and the top b2, but the labeling doesn’t matter in this case. The top could be called b1 and the bottom b2.
When using the calculator, “over 2” means divide by 2.
A note about order of operations: In this calculation, the 20.4 and 14.5 need to be added before the sum can be divided by 2. There are two ways to accomplish this:
- Use brackets on your calculator to calculate 20.4 + 14.5 before dividing by 2
- Use the equal sign after 20.4 + 14.5. Once the equal sign is pressed, the numbers are added, and you can divide the total by 2.
The sample calculation below uses brackets.
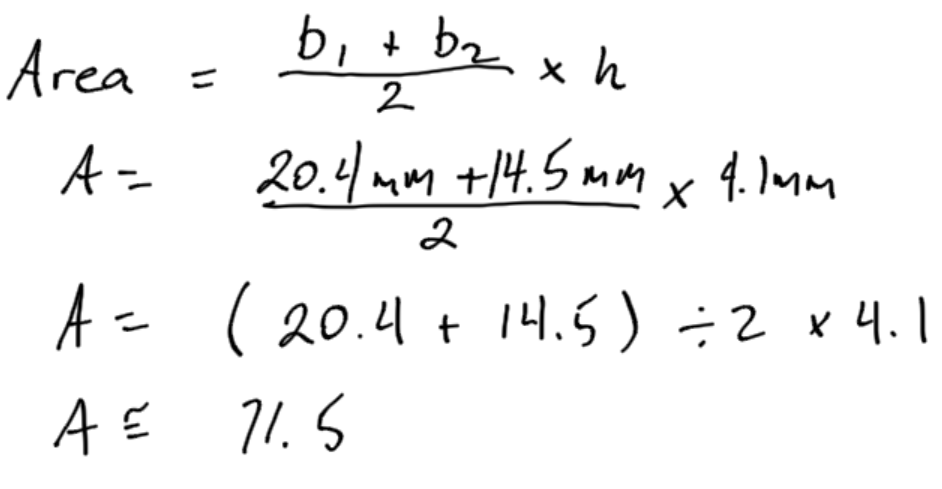
Example 5
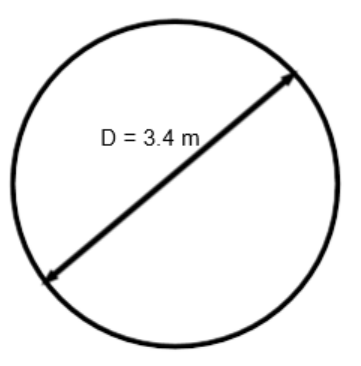

In this example, the diameter is given. The area formula for a circle calls for radius. We must convert the diameter into a radius by dividing it in half before using it in the formula.
Example 6

In some questions, it is necessary to find a total area, and subtract an inner area. In this example, to find the shaded area, we can find the area of the larger rectangle and subtract the area of the smaller rectangle.

Example 6a for the construction trades
When figuring the surface are of the shape above, only with uniform width, it is a shortcut to consider the centre line length. The centre line length is an imaginary line that travels through the centre of the shape. This is useful for calculations involving footings and basement walls.
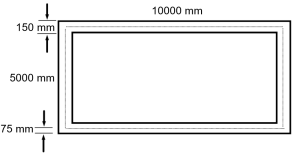
The short side centre line length is:
the outer dimension – half thickness – half thickness
or
the outer dimension – one thickness
(note the same can be achieved by taking the inner dimension and adding one thickness.)
Similarily, the long side centre line length is the outer dimension – one thickness.
Total centre line length is:
short side centre line length X 2 + long side centre line length X 2
For the above diagram, the total centre line length is:
To calculate the area, multiply the total centre line length by the thickness:
2.2 Areas of Parallelograms and Triangles
A parallelogram is a quadrilateral (it has four sides). The opposite sides of a parallelogram are parallel. It is also true that:
- the opposite sides of a parallelogram have equal length, and
- the opposite angles of a parallelogram have equal measure.
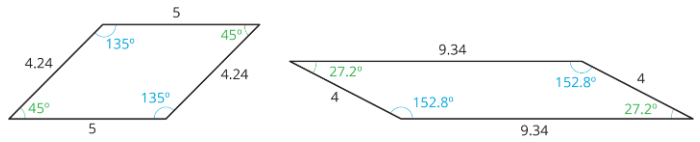
There are several strategies for finding the area of a parallelogram.
1. We can decompose and rearrange a parallelogram to form a rectangle.

2. We can enclose the parallelogram and then subtract the area of the two triangles in the corner.
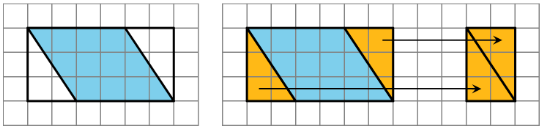
Both ways will work for any parallelogram. However, for some parallelograms the process of decomposing and rearranging requires a lot more steps than if we use a formula. Using a formula is a good shortcut, but if you don’t remember the formula, you can always rely on your ability to manipulate the image and use simpler formulas that you remember.
A parallelogram can always be decomposed into two identical triangles by a segment that connects opposite vertices.
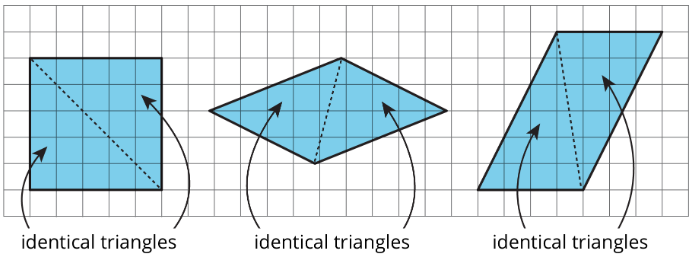
Going the other way around, two identical copies of a triangle can always be arranged to form a parallelogram, regardless of the type of triangle being used.
To produce a parallelogram, we can join a triangle and its copy along any of the three sides, so the same pair of triangles can make different parallelograms.
Here are examples of how two copies of both Triangle A and Triangle F can be composed into three different parallelograms.
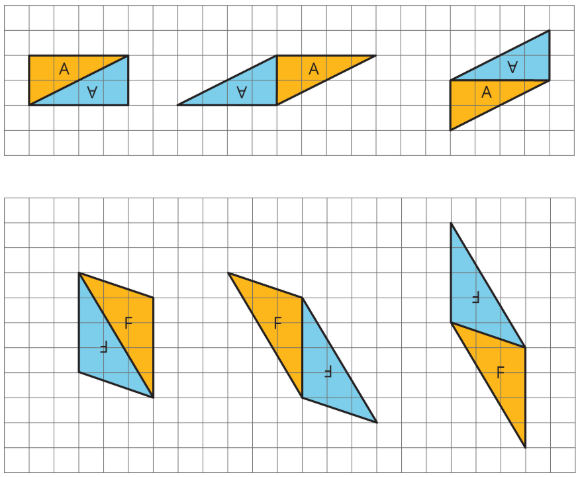
This special relationship between triangles and parallelograms can help us reason about the area of any triangle. If the area of a parallelogram is base times height, then it makes sense that the area of a triangle (which is half a parallelogram) is one half of the base times height.
– or –
Practice Exercises: Area
1. Are these statements true or false?
– A parallelogram has six sides.
– Opposite sides of a parallelogram are parallel.
– A parallelogram can have one pair or two pairs of parallel sides.
– All sides of a parallelogram must have the same length.
– All angles of a parallelogram must have the same measure.
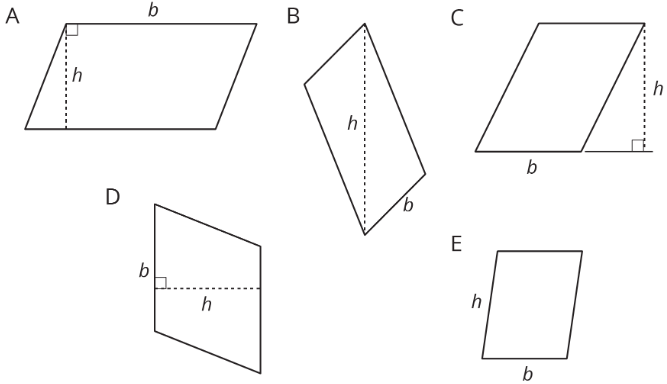
2. Five students labeled a base b and a corresponding height h for each of these parallelograms. Are all drawings correctly labeled? Explain how you know.
3. Find the area of the following shapes:
a. 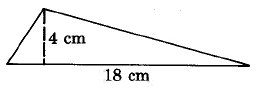 b.
b.
c.
d.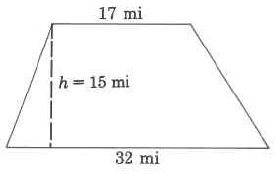 e.
e.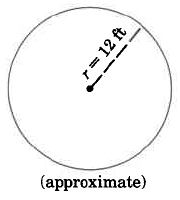
f.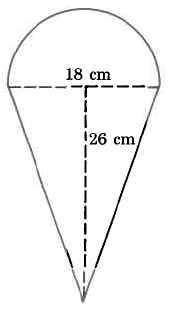 g.
g.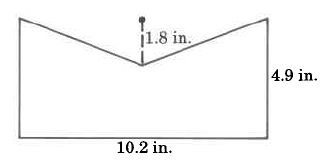
h. (Assume the following shape is vertically symmetric about the center.
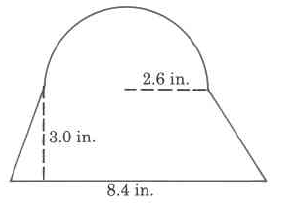 i.
i.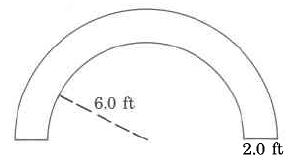
Solution:
1. F, T, F, F, F.
2. B and E are incorrect.
3. a) 36 cm2
b) 37.5 mm2
c) 13.3 in2
d) 368 mi2
e) 452 ft2
f) 361 cm2
g) 40.8 in2
h) 31.0 in2
i) 44 ft2
Topic 3: Surface Area
Surface area is the combined area of all the sides of a three dimensional shape.
Polyhedra
A polyhedron is a three-dimensional figure composed of faces. Each face is a filled-in polygon and meets only one other face along a complete edge. The ends of the edges meet at points that are called vertices.
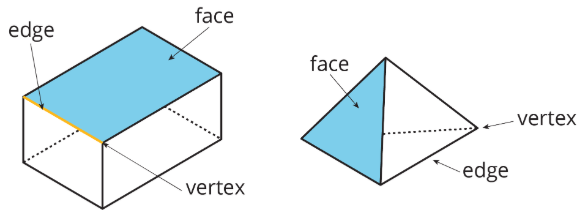
Polyhedra always encloses a three-dimensional region.
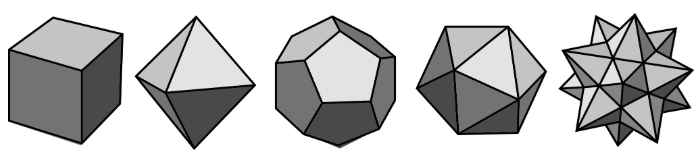
Here are pictures that represent polyhedra:
Here are pictures that do not represent polyhedra:
The surface area of a polyhedron is the sum of the areas of all the faces.
Because a net shows us all faces of a polyhedron at once, it can help us find the surface area. We can find the areas of all polygons in the net and add them.
A prism is a type of polyhedron with two identical faces that are parallel to each other and that are called bases. The bases are connected by a set of rectangles (or sometimes parallelograms).
A prism is named for the shape of its bases. For example, if the base is a pentagon, then it is called a “pentagonal prism.”
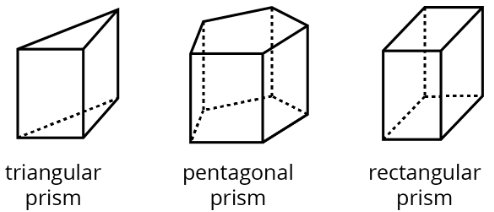
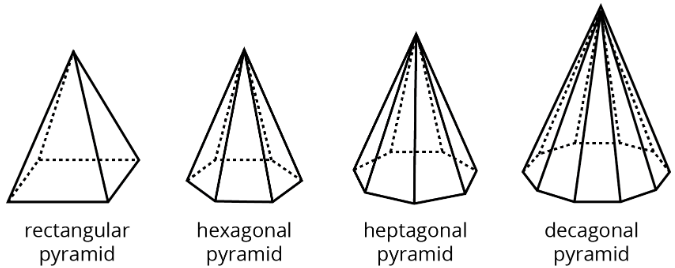
A pyramid is a type of polyhedron that has one special face called the base. All the other faces are triangles that all meet at a single vertex.
A pyramid is named for the shape of its base. For example, if the base is a pentagon, then it is called a “pentagonal pyramid.”
A net is a two-dimensional representation of a polyhedron. It is composed of polygons that form the faces of a polyhedron.
In a cube, every face shares its edges with 4 other squares. In a net of a cube, not all edges of the squares are joined with another edge. When the net is folded, however, each of these open edges will join another edge.
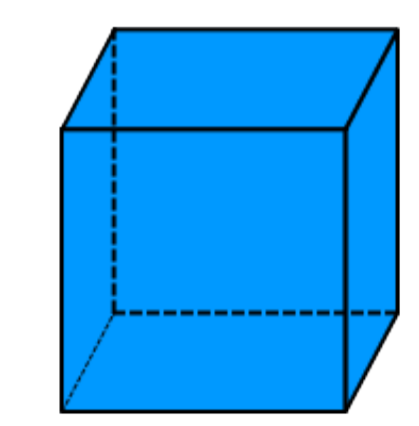
13. cube with 6 identical faces
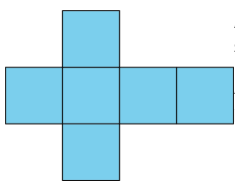
14. The net of the cube. Each side is connected by one shared line.
A net can be cut out and folded to make a model of the polyhedron.
Example 1
Find the surface area of this square pyramid.
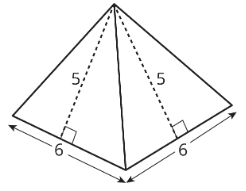
It is useful to help visualize all the sides flat. Then, the question just becomes finding the area of a bunch of basic shapes. Draw a net for the figure like so:

A square pyramid has a square and four triangles for its faces. Its surface area is the sum of the areas of the square base and the four triangular faces:
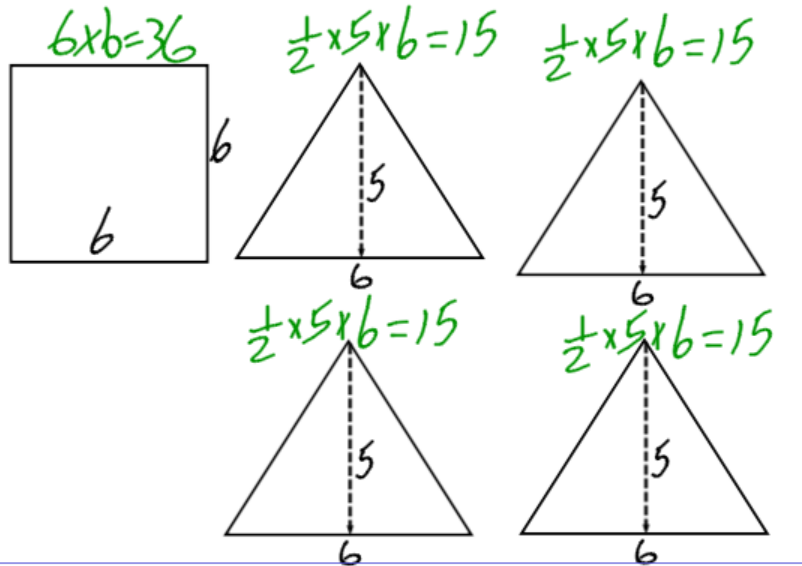
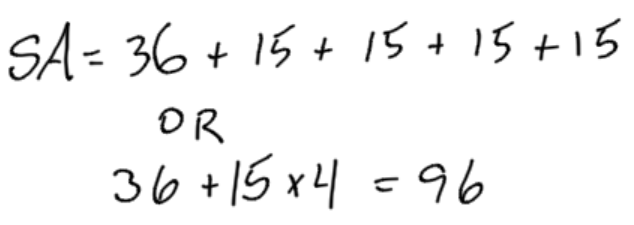
The surface area of this square pyramid is 96 square units.
A cylinder is a 3 dimensional shape that has a circular base.
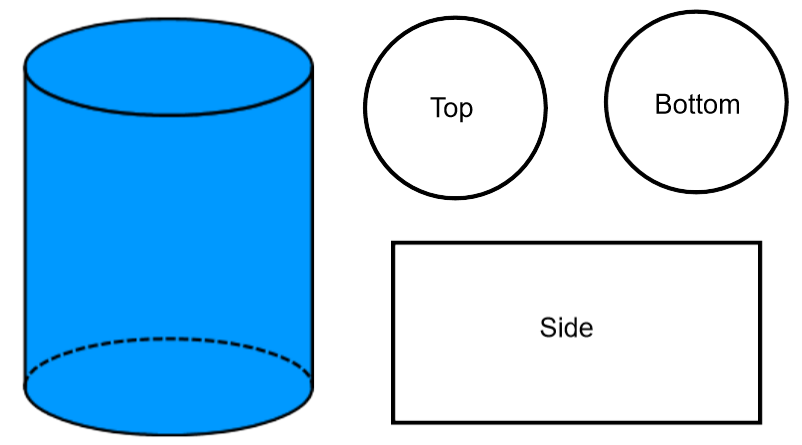
As seen in the diagram, the sides of the cylinder can be drawn as two circles for the top and bottom, and a rectangular side. The surface area of a cylinder is total area of the two circles and rectangle.
Example 2
Find the surface area of the following cylinder
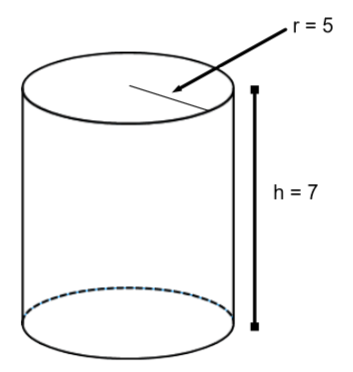
The cylinder can be broken down into the following circles (for top and bottom) with radius 5:
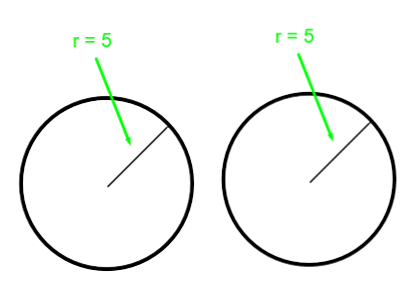
The area of one circle comes from the formula πr2
Area= πr2
Area= π×52≈ 78.54
Finding the dimensions of the side involves a trick. The height is obviously 7, from the original diagram. The width is the circumference of the circle. (Remember, the formula for the circumference is
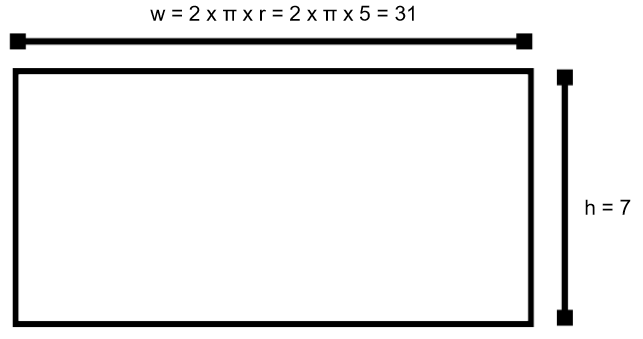
To calculate the width, us the formula for the circumference of the top or base: 2πr.
circumference=2πr
width=2×π×5≈31.42
The area of the rectangle is the length times the width:
7×31.42=219.94
The total area of the sides of the cylinder:
total surface area=area top+ area bottom +area side
total surface area=78.54+78.54+219.94
total surface area ≈ 377
Practice Exercises: Surface Area
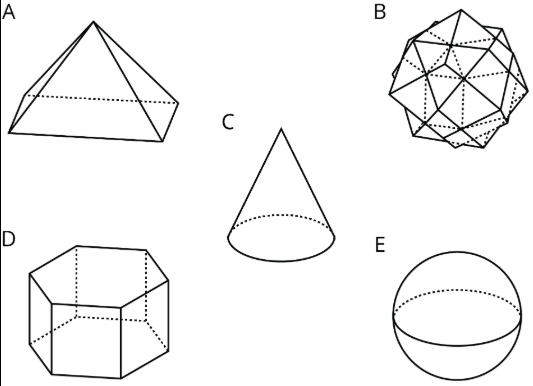
1. Which of the following shapes represent a polyhedron?
2. Is this polyhedron a prism, a pyramid, or neither? Explain how you know.
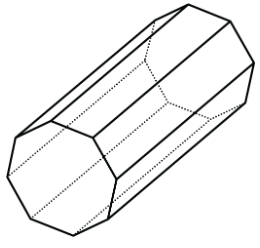
3. Here are two polyhedra and their nets. Label all edges in the net with the correct lengths. Find the surface area of polyhedron A.
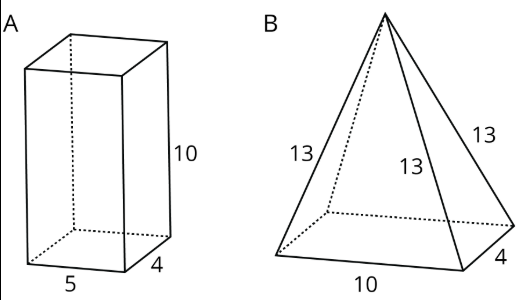
Challenge Question: Find the surface area of polyhedron B. (Hint: you will need to use Pythagoras’ Theorem to find the heights of the triangles.)
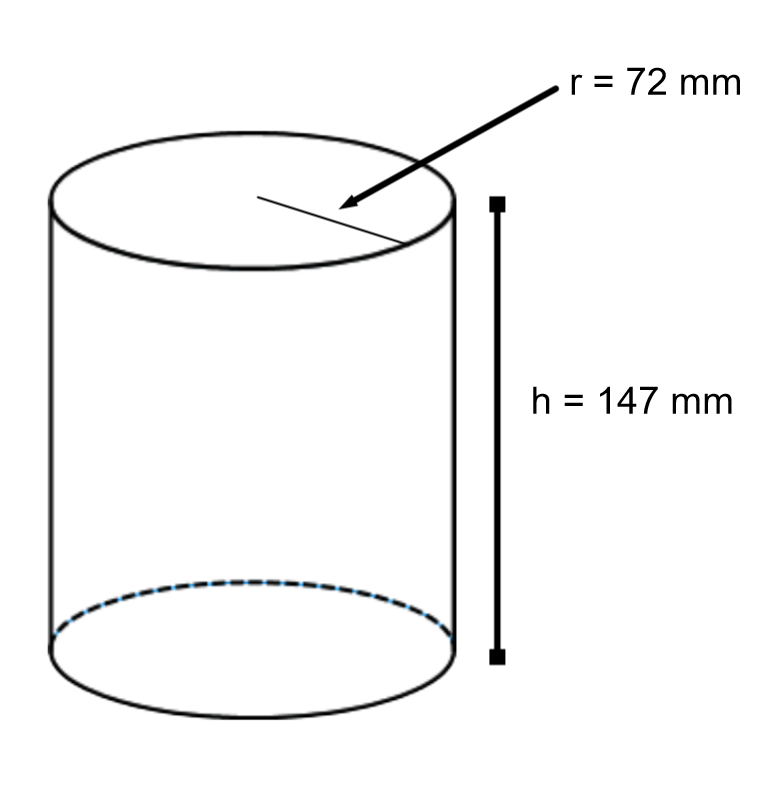
4. Calculate the surface area of the following cylinder
Solution:
1. A, B, D
2. Prism because does not come to a tip, sides are not triangles.
3. Surface area A = 220 square units, Surface area B = 211 square units.
4. Surface area = 99,073 square mm.
Topic 4: Volume
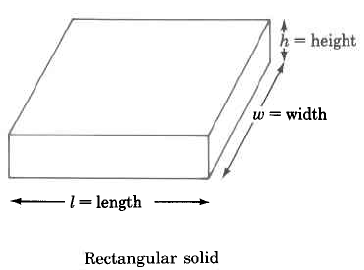
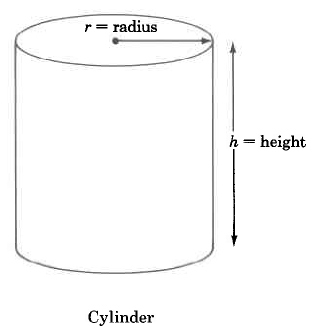
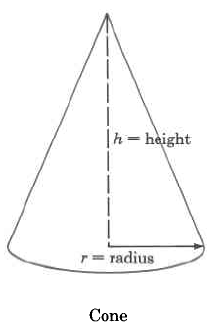
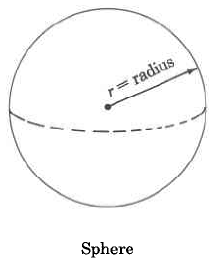
Volume Formulas
|
|
Figure |
Volume Formula |
|
|
Rectangular solid |
|
|
|
Sphere |
|
|
|
Cylinder |
|
|
|
Cone |
|
Example 1
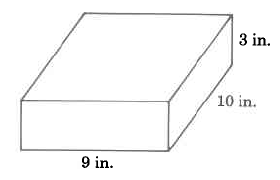
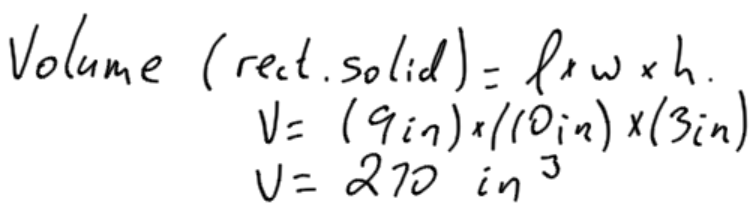
Example 2
Find the volume of this sphere:
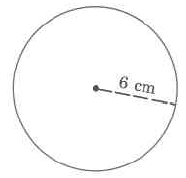
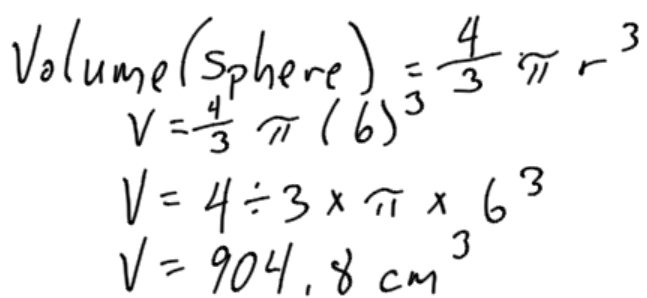
Example 3
Find the volume of this cylinder:
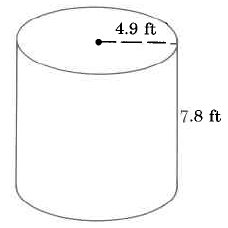
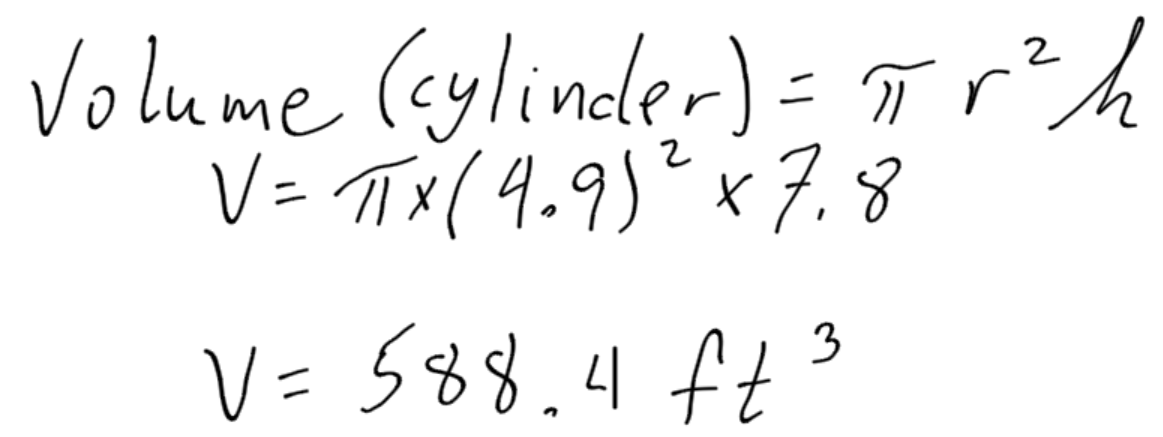
Example 4
Find the volume of this cone:
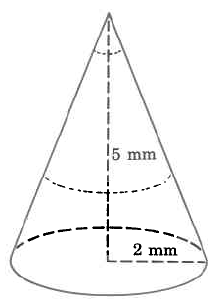
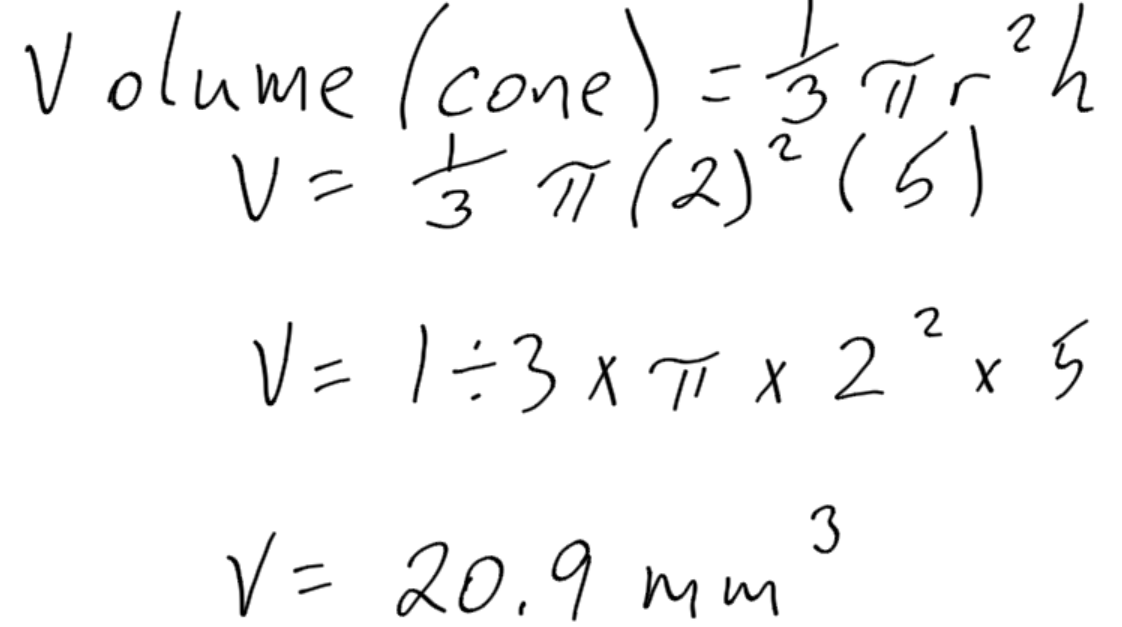
Practice Exercises: Volume
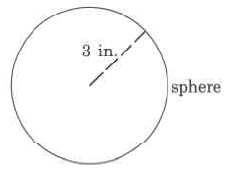
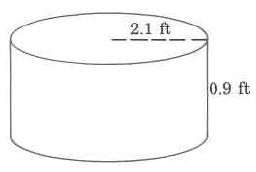
1. Find the volume of the following shapes:
a.
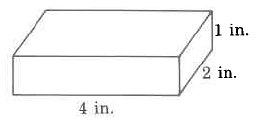
b.
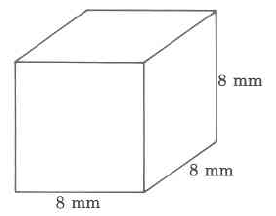
c.
d.
e.
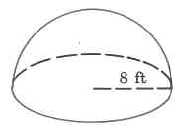
f.
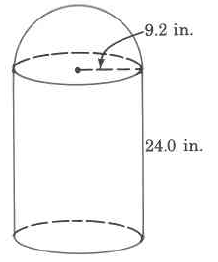
g.
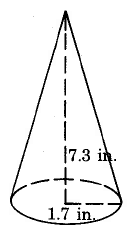
h.

i.
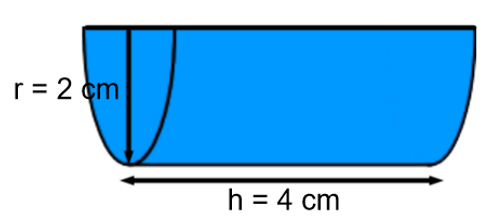
Solution:
1. a) 8 in3
b) 512 mm3
c) 113 in3
d) 12.5 ft3
e) 1072 ft3
f) 8012.6 in3
g) 22.1 in3
h) 64.3 ft3
i) 25.13 cm3
Topic 5: Pythagoras’ Theorem
Introduction:
In this section you will learn about right-angle triangle properties, proportionality, and the Pythagorean Theorem. Throughout the section you will be presented with concepts and examples, as well as opportunities to practice.
5.1 Right Angle Triangle Properties
An angle is formed when two straight paths cross. Consider this story: you walk along a straight path, and so does your friend. At first you both are so far apart that you can’t see each other. But as you walk along you get closer and closer until you meet together. Your meeting place is called the vertex.
The interesting part about angles is at the beginning of the journey, you are far from your friend. Halfway through your journey, your friend is closer, and at the end of the journey there is no distance between you and your friend. Throughout the journey you were a changing distance from each other, but the angle of your paths did not change.

Notice the paths on the left form a smaller angle than the paths on the right. The size of an angle is measured in degrees.
Types of Angles
Angles can be grouped according to how large they are. Special angles are:
- The right angle: One half of a square is a right angle. Notice the right angle symbol (a small box.) The symbol for degrees is the small circle to the upper right of the number, and a right angle is 90˚ (degrees.)
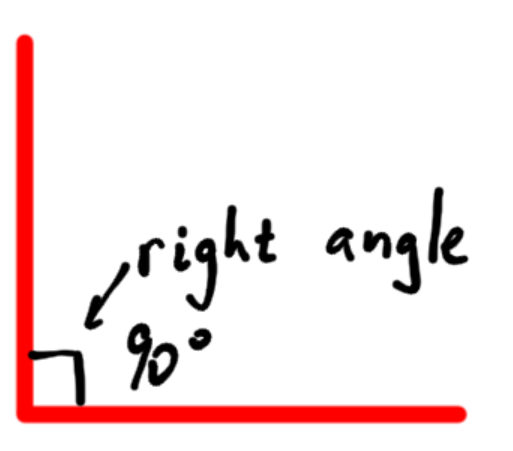
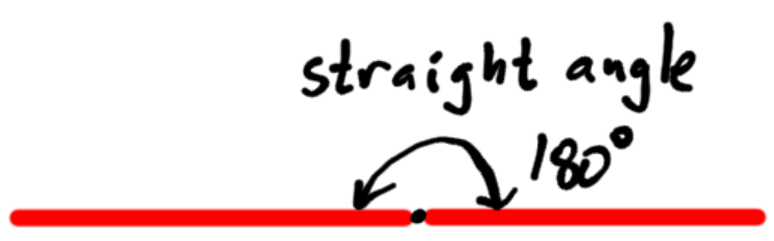
- The Straight Angle: The straight angle is essentially a line. In the story above, it would be if you and your friend were headed straight on toward each other.
- Acute Angle: An acute angle is less than 90 degrees.
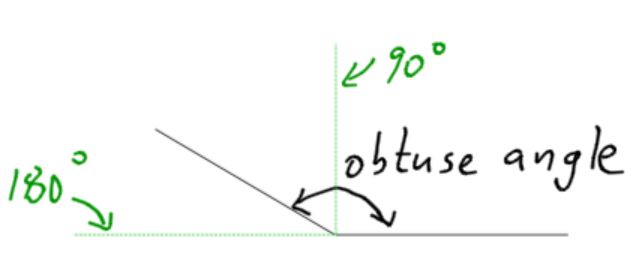
- Obtuse Angle: An obtuse angle is greater than 90 degrees, but less than 180 degrees (a straight line.)
Examples:
Label the following angles:
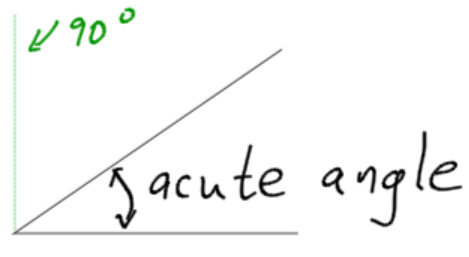
Related Angles
Two angles are related when they add up to either 90 or 180 degrees. Two angles that add to 90 degrees are complimentary. Two angles that add to 180 degrees are supplementary.
Examples:
1. Angles 25˚ and 65˚ are complimentary because 25 + 65 = 90
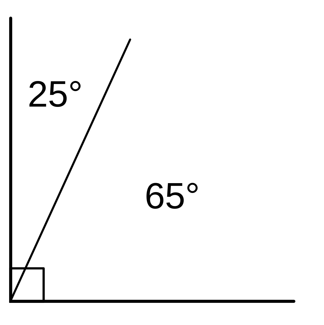
2. Angles 45˚ and 135˚ are supplementary because 45 + 135 = 180
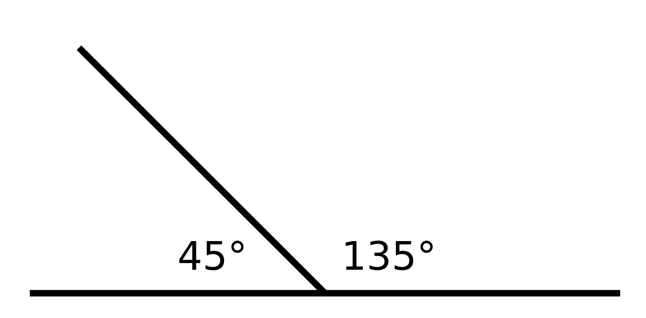
Types of Triangles
Triangles are classified into three types: the same as angles.
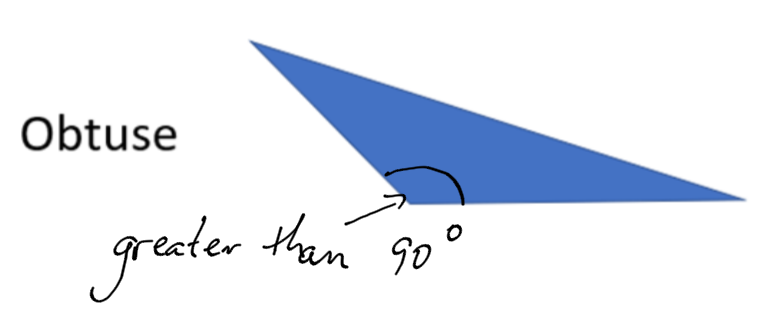
An obtuse triangle has one angle that is greater than 90 degrees (one obtuse angle.)
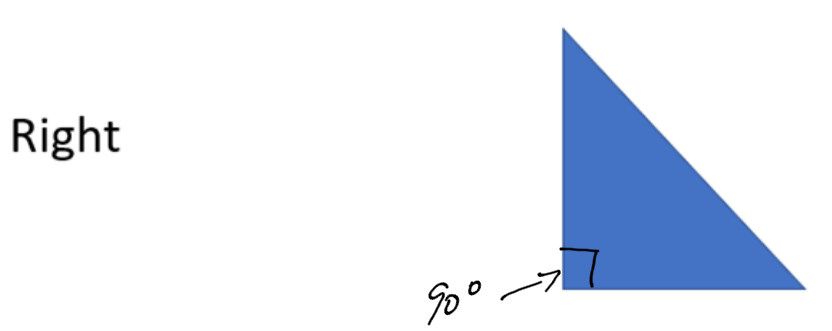
A right triangle has one angle that is exactly 90 degrees (one right angle.)
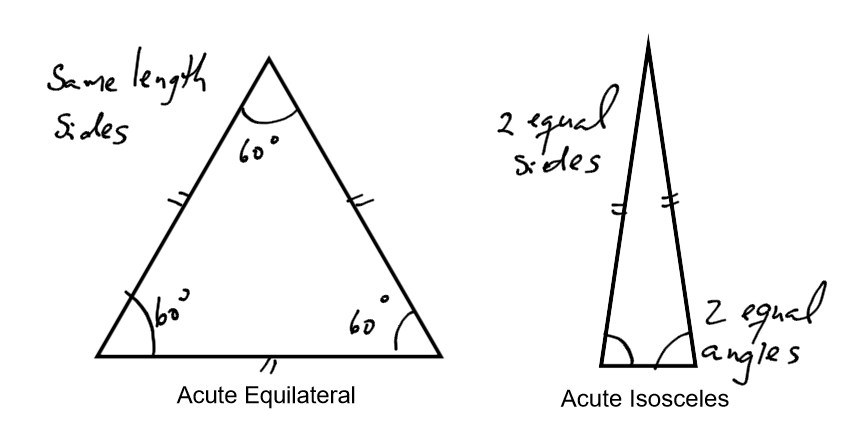
An acute triangle has all three angles less than 90 degrees (three acute angles). Above, the triangle on the left is called equilateral because all the sides are the same length. The triangle on the right is called isosceles because two of the sides are the same length.
Examples:
1. How large, in degrees, is the unknown angle?
a)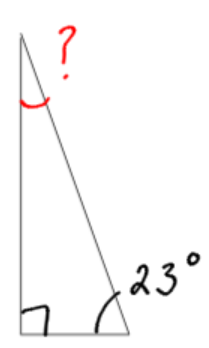
Although it isn’t written, one of the angles is 90 degrees, because it is marked with the box. The other angle is 23 degrees.
180 total degrees – 90 degrees – 23 degrees = 67 degrees. There are 67 degrees left for the unknown angle.
b)
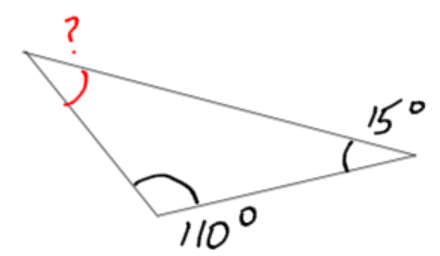
180 total degrees – 110 degrees – 15 degrees = 55 degrees. There are 55 degrees left for the unknown angle.
5.2 Pythagorean Theorem
Instructions
- Go through the content and examples with the group, leaving opportunities for questions.
- Have students complete the practice exercises independently, then take up the answers.
The two shorter sides of a right triangle (the sides that form the right angle) are the legs and the longer side (the side opposite the right angle) is the hypotenuse. For the Pythagorean Theorem, the legs are “a” and “b” and the hypotenuse is “c”.
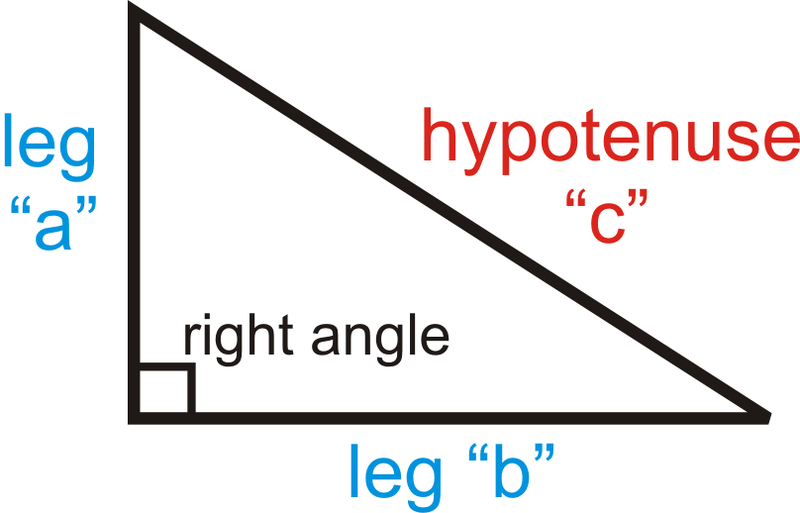
Pythagorean Theorem:
Given a right triangle with legs of lengths a and b and a hypotenuse of length c,
The converse of the Pythagorean Theorem is also true. It allows you to prove that a triangle is a right triangle even if you do not know its angle measures.
If the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
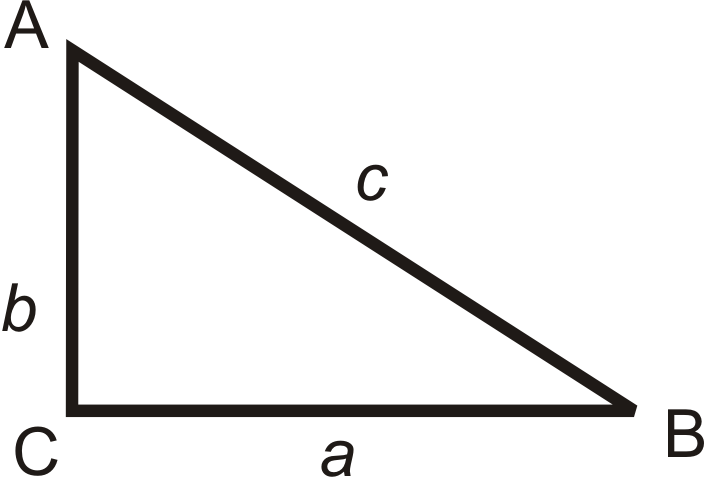
Notice in the above diagram, Labeling the triangle is as follows:
- Angles are labeled with capital letters
- Sides are labeled with small letters
- The side and the opposite angle have the same letter.
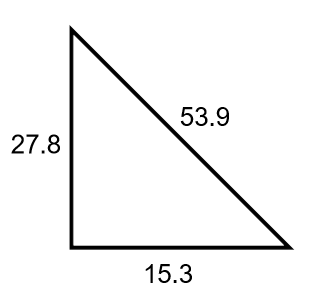
Example:
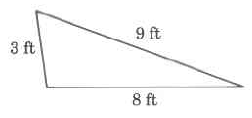
Is the following triangle a right angle triangle?
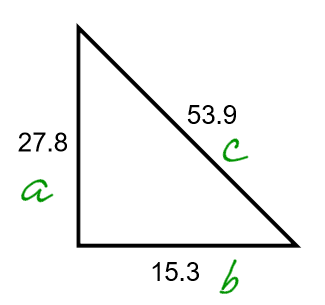
Label the sides of the triangle. The Hypotenuse must be labeled c:
Test the Pythagorean theorem to see if both sides of the equation are equal. If both sides are equal, the triangle is a right angle triangle.
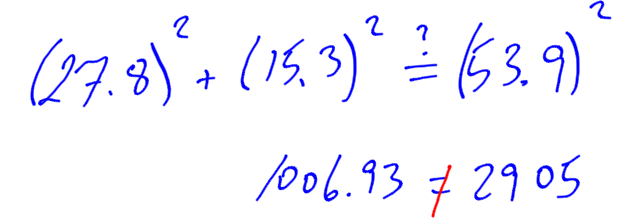
Since 1006 does not equal 2905, the triangle is not a right angle triangle.
Learning Task: Outcome 5 Test
Complete the Essentials 1 Math: Space and Shape Chapter Quiz on Brightspace.