35 Outcome 6: Electrical Power

Introduction:

• In this module, we will review comparisons between mechanical and electrical energy and power, how to calculate electrical power within a circuit, and how to apply the energy cost formula. This chapter will include class discussions, articles to be reviewed, review questions, and a cumulative test.

Topic 1: Electric Power

Prerequisite Skills:

• Solving equations and combining two equations by substitution will be discussed. It may be a good opportunity to review points of algebra.

We know that horsepower is a rate of doing work. Electrical power is also referred to as the rate of doing work. A more correct definition of power is the rate at which electrical energy can be converted to heat, light, acoustic, or mechanical energy. The energy is this case must be thought of as work not as output. The metric unit for energy is newtons – meter.

One Newton – metre was called a “joule” for ease of use. Therefore, if power is a rate doing work we can see that:

 

Topic 2: Watt’s Law

Since electrical power is measured in watts and it has a direct relationship with voltage and amperage, we should be able to use it in a mathematical formula. The formula is:

This formula is similar in format to Ohm’s law ( E = I X R ) so we can use the same tradesperson’s triangle method of transposing the equation:

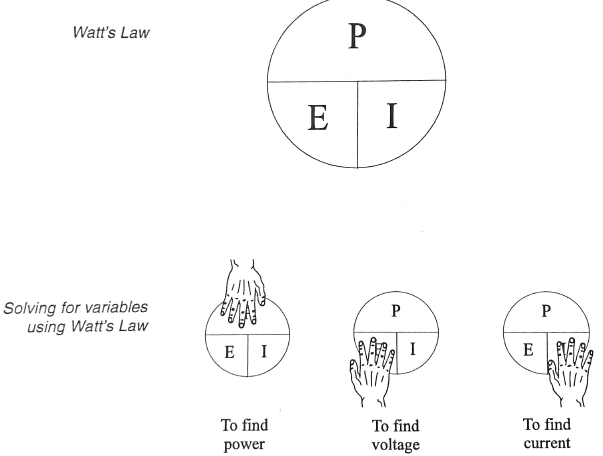
we also know ohms law as:

we can combine the two to include resistance in a formula:

 

another formula is:

We can now solve for the power in a circuit using any two variables.

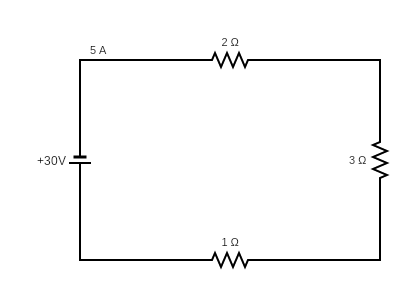
Example 1

Use all three power equations to find power in this circuit and see if they confirm each other.

-or-

-or-

 

Example 2

A radio is rated 36 watts. How much force is needed to push 3 amps through it?

Example 3

Power ratings for heating and lighting (including toasters ovens, hair dryers, etc.) are usually rated or measured in watts. If this power rating was in mechanical terms, what would the appliance be rated in?

Answer: Horsepower.

 

Example 4

What would a 7 horsepower motor be rated at in watts?

 

Example 5

What horsepower is a 200 kW motor?

 

Topic 3: Electrical Energy

Electrical energy is converted to heat, light, or mechanical energy to create power.

Electrical energy in the above equation is work.

Electrical utilities have another term also called electrical energy but with a different meaning. This can be somewhat confusing but can be explained by the fact that this electrical energy is a unit of measurement.

First, although we say we purchase and sell power what we really are selling is electrical energy.

“Power” is a rating of a motor or load. An example of this is a two kilowatt motor. This indicates how fast the energy is consumed (a 2 kW motor uses energy faster than a 1 kW motor.)

Electrical energy is measured in kilowatt hours. This is how we commercially sell energy.

 

 

Example 6

If a 2 kW motor ran for six hours how much energy is used?

Topic 4: Energy Cost Calculations

Since utilities are in the business of selling electrical energy, they must have some method of knowing how much energy is used by each customer. We do this by using a meter that measures watts and hours. In other words, the power consumed by a customer over a time frame.

Since the water – hour is a very small unit, we charged by the kWh instead. The formula for cost is:

There are three things to remember when doing cost calculations:

• If you get your power (E X I) in watts, you must divide the equation by 1000 to get kilowatt hours.
• Energy is charged in cents per kWh to get dollars. In our equation, we must convert cents to dollars. For example, 7 cents, or $0.07 = 0.07 dollars.
• Since energy is in kilowatt hours, we must convert days, weeks, etc. into hours.

Example 7

What is the cost to operate for three hours at 5.6 cents per kWh

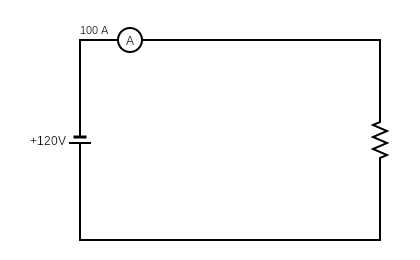
Notice, in this case, we kept the energy in kWh to simplify the cost calculation.  Therefore, there was no need to divide by 1000.

Example 8

What is the cost to operate for six weeks 12 hours per day at 5.6 cents per kWh

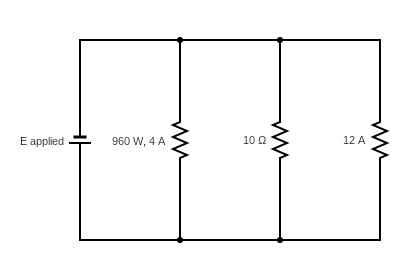
E3=960W4A=240V

To operate for 6 weeks, 12 hours per day, at 5.6 cents per kWh:

Topic 5: Line Voltage and Power Loss

We have learned in the previous modules that current needs a push (volts) to overcome the resistance in conductors. Since all conductors possess resistance, some voltage and power is lost in the conductors that feed a load.

The power and voltage losses in the conductor itself will be covered in this topic. You will see how the resistance of a conductor effects the voltage and power available to a load.

Voltage Loss in the Line Wires

A two-wire circuit is a circuit that provides a path to and from a load.

Examples:

• A Hi-con line to a farm transformer with the earth return (ground grid)
• A duplex service to a streetlight.

In both examples, resistance in the conductors will affect the circuit.

We will represent the line wires as being in series with the source and show the affect a voltage drop across a resistor (the lines) has on the circuit.

Note: when we solve two-wire circuits, both wires have the same amount of resistance unless otherwise stated.

Practice Exercises

Find the line current in the following circuits

a)

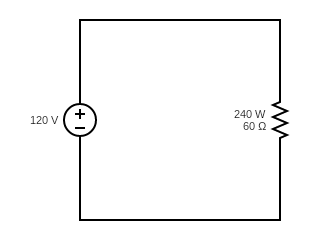
b)

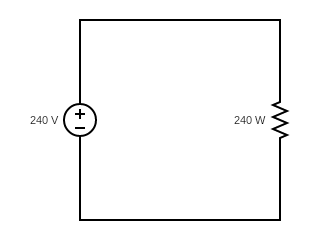
c)

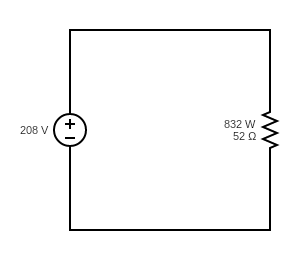
d)

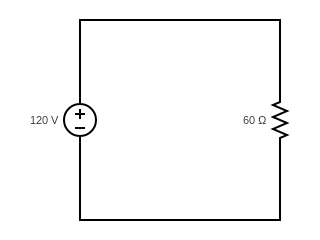
e)

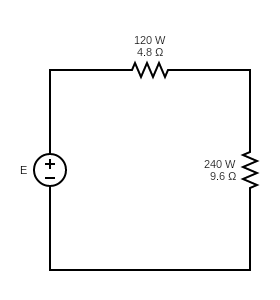
f)

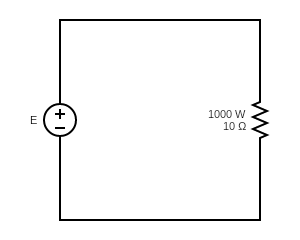
g)

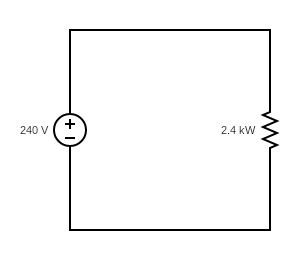
h)

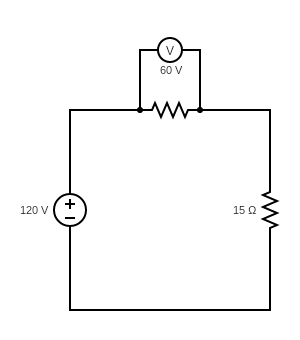
Answer Key

a 2, b 1, c 4, d 2, e 5, f 10, g 10, h 4